题目内容
(本题满分14分)
设函数
⑴当 且函数
且函数 在其定义域上为增函数时,求
在其定义域上为增函数时,求 的取值范围;
的取值范围;
⑵若函数 在
在 处取得极值,试用
处取得极值,试用 表示
表示 ;
;
⑶在⑵的条件下,讨论函数 的单调性。
的单调性。
【答案】
(1) 。(2)
。(2) ;
;
(3)当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 。
。
【解析】本试题主要是考查了导数在研究函数单调性中的运用。
⑴因为当 且函数
且函数 在其定义域上为增函数时,则可知导函数恒大于等于零,得到
在其定义域上为增函数时,则可知导函数恒大于等于零,得到 的取值范围;
的取值范围;
⑵若函数 在
在 处取得极值,则求解导数可知导函数在该点的到数值为零。
处取得极值,则求解导数可知导函数在该点的到数值为零。
⑶在⑵的条件下, ,然后对于参数a分情况得到函数
,然后对于参数a分情况得到函数 的单调性。
的单调性。
解:(1)当 时,函数
时,函数 ,其定义域为
,其定义域为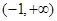 。
。
 。
。 函数
函数 是增函数,
是增函数,
 当
当 时,
时, 恒成立。 ……………………………………2分
恒成立。 ……………………………………2分
即当 时,
时, 恒成立。
恒成立。
 当
当 时,
时,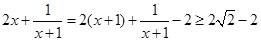 ,且当
,且当 时取等号。
时取等号。
 的取值范围为
的取值范围为 。………………………………………………………………4分
。………………………………………………………………4分
(2) ,且函数
,且函数 在
在 处取得极值,
处取得极值,

此时 ………………………………………………6分
………………………………………………6分
当 ,即
,即 时,
时, 恒成立,此时
恒成立,此时 不是极值点。
不是极值点。
 ………………………………………………………………………8分
………………………………………………………………………8分
(3)由 得
得
①当 时,
时,
 当
当 时,
时,
当 时,
时,
 当
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 。……………………10分
。……………………10分
②当 时,
时,
 当
当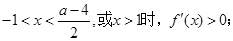
当
 当
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 。
。
③当 时,
时,
 当
当
当
 当
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 。
。
……………………………………………………13分
综上所述: 当
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 。
。
………………………………………………………………14分

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).