题目内容
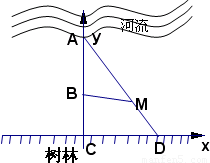
 树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
(1)求兔子被狼吃掉的点的区域面积S(a);
(2)若兔子要想不被狼吃掉,求θ(θ=∠DAC)的取值范围.
解:(1)如图建立坐标系xOy,设 A(0,2a),B(0,a),M(x,y),
由 ,得
,得 .所以M在以
.所以M在以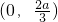 为圆心,半径为
为圆心,半径为 的圆及其内部.
的圆及其内部.
所以, .-------(8分)
.-------(8分)
(2)设lAD:y=kx+2a(k≠0),由 ,
,
可得 0<∠ADB< ,所以,
,所以, .---------(6分)
.---------(6分)
分析:(1)如图建立坐标系xOy,设 A(0,2a),B(0,a),M(x,y),由 ,求得
,求得 .由此求得圆的面积S(a)的值.
.由此求得圆的面积S(a)的值.
(2)设lAD:y=kx+2a(k≠0),由 求得斜率k的范围,即可求得θ的范围.
求得斜率k的范围,即可求得θ的范围.
点评:本题主要考查圆的标准方程,直线和圆的位置关系,直线的倾斜角和斜率的关系,属于中档题.
由
 ,得
,得 .所以M在以
.所以M在以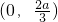 为圆心,半径为
为圆心,半径为 的圆及其内部.
的圆及其内部.所以,
 .-------(8分)
.-------(8分)(2)设lAD:y=kx+2a(k≠0),由
 ,
,可得 0<∠ADB<
 ,所以,
,所以, .---------(6分)
.---------(6分)分析:(1)如图建立坐标系xOy,设 A(0,2a),B(0,a),M(x,y),由
 ,求得
,求得 .由此求得圆的面积S(a)的值.
.由此求得圆的面积S(a)的值.(2)设lAD:y=kx+2a(k≠0),由
 求得斜率k的范围,即可求得θ的范围.
求得斜率k的范围,即可求得θ的范围.点评:本题主要考查圆的标准方程,直线和圆的位置关系,直线的倾斜角和斜率的关系,属于中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.