Question

已知椭圆C₁的方程为

x2

4

+y²=1，双曲线C₂的左、右焦点分别为C₁的左、右顶点，而C₂的左、右顶点分别是C₁的左、右焦点．
（Ⅰ）求双曲线C₂的方程；
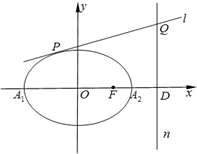
（Ⅱ）若直线l：y=kx+

2

与椭圆C₁及双曲线C₂都恒有两个不同的交点，且l与C₂的两个交点A和B满足

OA

•

OB

＜6（其中O为原点），求k的取值范围．

Answer 1

（Ⅰ）设双曲线C₂的方程为

x2

a2

-

y2

b2

=1，则a²=4-1=3，再由a²+b²=c²得b²=1．
故C₂的方程为

x2

3

-y²=1．
（II）将y=kx+

2

代入

x2

4

+y²=1得（1+4k²）x²+8

2

kx+4=0
由直线l与椭圆C₁恒有两个不同的交点得△1=(8

2

)2k2-16（1+4k²）=16（4k²-1）＞0，
即k²＞

1

4

①
将y=kx+

2

代入

x2

3

-y²=1得（1-3k²）x²-6

2

kx-9=0．
由直线l与双曲线C₂恒有两个不同的交点A，B得

1-3k2≠0 △2=(-6 2 k)2+36(1-3k2)=36(1-k2)＞0.

即k²≠

1

3

且k²＜1．②
设A（x_A，y_A）B（x_B，y_B），则x_A+x_B=

6 2 k

1-3k2

，x_A•x_B=

-9

1-3k2

．
由

OA

•

OB

＜6得x_Ax_B+y_Ay_B＜6，
而x_Ax_B+y_Ay_B=x_Ax_B+（kx_A+

2

）（kx_B+

2

）
=（k²+1）x_Ax_B+

2

（x_A+x_B）+2
=（k²+1）•

-9

1-3k2

+

2

k•

6 2 k

1-3k2

+2
=

3k2+7

3k2-1

．
于是

3k2+7

3k2-1

＜6，即

15k2-13

3k2-1

＞0．
解此不等式得k²＞

13

15

或k²＜

1

3

．③
由①、②、③得

1

4

＜k²＜或

13

15

＜k²＜1．
故k的取值范围为（-1，-

13 15

）∪（-

3

3

，-

1

2

）∪（

1

2

，

3

3

）∪（

13 15

，1）．