Question

在空间中，若射线OA、OB、OC两两所成角都为，且OA=2，OB=1，则直线AB与平面OBC所成角的大小为________．

Answer 1

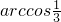
分析：由已知中∠AOB=60°、OA=2，OB=1，由余弦定理，我们易得AB⊥OB，令OC=2，我们可进而得到CB⊥OB，∠ABC即为AB与面OBC所成的角，利用余弦定理解三角形ABC即可得到直线AB与平面OBC所成角的大小．
解答：由∠AOB=60°、OA=2，OB=1
得AB⊥OB 不妨取OC=2，则CB⊥OB
∠ABC即为AB与面OBC所成的角
AB=BC= AC=2
由余弦定理，
cos∠ABC===
∴所求角的大小为arccos
故答案为：arccos．
点评：本题考查的知识点是直线与平面所成的角，其中根据已知确定，∠ABC即为AB与面OBC所成的角，是解答本题的关键．