题目内容
已知函数f（x）=x3-3x及y=f（x）上一点P（1，-2），过点P作直线l．
（1）求使直线l和y=f（x）相切且以P为切点的直线方程；
（2）求使直线l和y=f（x）相切且切点异于P的直线方程．
解：（1）由f（x）=x3-3x得，f′（x）=3x2-3，
过点P且以P（1，-2）为切点的直线的斜率f′（1）=0，
∴所求直线方程为y=-2．
（2）设过P（1，-2）的直线l与y=f（x）切于另一点（x0，y0），
则f′（x0）=3x02-3．
又直线过（x0，y0），P（1，-2），
故其斜率可表示为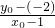
=
，
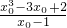又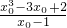=3x02-3，
即x03-3x0+2=3（x02-1）•（x0-1），
解得x0=1（舍）或x0=-
，
故所求直线的斜率为k=3×（
-1）=-
，
∴y-（-2）=-（x-1），
即9x+4y-1=0．
分析：（1）由已知可得斜率函数为f′（x）=3x2-3，进而求出所过点切线的斜率，代入点斜式公式即可．
（2）设另一切点为（x0，y0），求出该点切线方程，再由条件计算．
点评：本题较为简单，主要考查的是直线的点斜式方程的求解，掌握好这一方法即可．
过点P且以P（1，-2）为切点的直线的斜率f′（1）=0，
∴所求直线方程为y=-2．
（2）设过P（1，-2）的直线l与y=f（x）切于另一点（x0，y0），
则f′（x0）=3x02-3．
又直线过（x0，y0），P（1，-2），
故其斜率可表示为
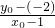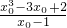=，又
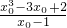=3x02-3，即x03-3x0+2=3（x02-1）•（x0-1），
解得x0=1（舍）或x0=-
，故所求直线的斜率为k=3×（
-1）=-，∴y-（-2）=-
（x-1），即9x+4y-1=0．
分析：（1）由已知可得斜率函数为f′（x）=3x2-3，进而求出所过点切线的斜率，代入点斜式公式即可．
（2）设另一切点为（x0，y0），求出该点切线方程，再由条件计算．
点评：本题较为简单，主要考查的是直线的点斜式方程的求解，掌握好这一方法即可．
练习册系列答案
名校课堂系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|