题目内容
已知函数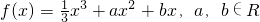 .
.
(1)曲线C:y=f(x)经过点P(1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(2)在(1)的条件下试求函数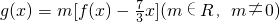 的极小值;
的极小值;
(3)若f(x)在区间(1,2)内存在两个极值点,求证:0<a+b<2.
(1)解:对函数求导可得,f′(x)=x2+2ax+b,
由题设知: 解得
解得 (4分)
(4分)
(2)解:由(1)知 ,g′(x)=mx(x-
,g′(x)=mx(x- ),
),
当m>0时,g(x)在(-∞,0),( ,+∞)上递增,在(0,
,+∞)上递增,在(0, )上递减,
)上递减,
所以g(x)的极小值为g( )=-
)=- m;
m;
当m<0时,g(x)在(-∞,0),( ,+∞)上递减,在(0,
,+∞)上递减,在(0, )上递增,
)上递增,
所以g(x)的极小值为g(0)=0;(8分)
(3)证明:因为f(x)在区间(1,2)内存在两个极值点,所以f′(x)=0,即x2+2ax+b=0在(1,2)内有两个不等的实根.
∴ (11分)
(11分)
由 (1)+(3)得a+b>0,由(4)得a+b<a2+a,
∴-2<a<-1,又 ,
,
∴a+b<2.
故a+b的取值范围是(0,2)(14分)
分析:(1)曲线在P(1,2)处的切线与y=2x+1平行等价于函数在该点的导数为2,f(1)=2,代入可求a,b
(2)由(1)知 ,g′(x)=mx(x-
,g′(x)=mx(x- ),分类讨论:分m>0时,m<0时两种情况讨论,g(x)的单调性,进而可求g(x)的极小值
),分类讨论:分m>0时,m<0时两种情况讨论,g(x)的单调性,进而可求g(x)的极小值
(3)由题意可得f′(x)=0即x2+2ax+b=0在(1,2)内有两个不等的实根,根据二次方程的实根分布可求
点评:本题考查函数的极值与导数之间的关系,考查函数有极值的条件,考查学生的转化与化归思想.
由题设知:
 解得
解得 (4分)
(4分)(2)解:由(1)知
 ,g′(x)=mx(x-
,g′(x)=mx(x- ),
),当m>0时,g(x)在(-∞,0),(
 ,+∞)上递增,在(0,
,+∞)上递增,在(0, )上递减,
)上递减,所以g(x)的极小值为g(
 )=-
)=- m;
m;当m<0时,g(x)在(-∞,0),(
 ,+∞)上递减,在(0,
,+∞)上递减,在(0, )上递增,
)上递增,所以g(x)的极小值为g(0)=0;(8分)
(3)证明:因为f(x)在区间(1,2)内存在两个极值点,所以f′(x)=0,即x2+2ax+b=0在(1,2)内有两个不等的实根.
∴
 (11分)
(11分)由 (1)+(3)得a+b>0,由(4)得a+b<a2+a,
∴-2<a<-1,又
 ,
,∴a+b<2.
故a+b的取值范围是(0,2)(14分)
分析:(1)曲线在P(1,2)处的切线与y=2x+1平行等价于函数在该点的导数为2,f(1)=2,代入可求a,b
(2)由(1)知
 ,g′(x)=mx(x-
,g′(x)=mx(x- ),分类讨论:分m>0时,m<0时两种情况讨论,g(x)的单调性,进而可求g(x)的极小值
),分类讨论:分m>0时,m<0时两种情况讨论,g(x)的单调性,进而可求g(x)的极小值(3)由题意可得f′(x)=0即x2+2ax+b=0在(1,2)内有两个不等的实根,根据二次方程的实根分布可求
点评:本题考查函数的极值与导数之间的关系,考查函数有极值的条件,考查学生的转化与化归思想.

练习册系列答案
相关题目
 .
.
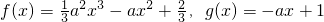 .
. .
. .
. 的极小值;
的极小值;