题目内容
 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,用茎叶图表示这两组数据.
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,用茎叶图表示这两组数据.
(Ⅰ)现要从中选派一人参加数学竞赛,从平均数与方差的角度考虑,你认为选派哪位学生参加合适?
(Ⅱ)若将频率为概率,对乙同学在今后的3次数学竞赛成绩进行预测,记这3次成绩中高于80分的次数为ξ,求ξ的分布列及数学期望Eξ.
解:(Ⅰ)因为 由题意可得: =
=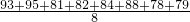 =85,
=85,
 =
=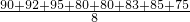 =85,
=85,
所以s甲2=35.5,s乙2=41,
∴s甲2<s乙2,
∴乙的成绩较稳定,派乙参赛比较合适. …7分
(II) 记“乙同学在一次数学竞赛中成绩高于80分”为事件A,
则P(A)=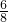 =
= .
.
随机变量ξ 的可能取值为0、1、2、3,且ξ~B(3, ).
).
∴P(ξ=k)=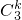 (
(  )k(
)k(  )3-k,k=0,1,2,3.
)3-k,k=0,1,2,3.
所以变量ξ 的分布列为:
Eξ=0× +1×
+1× +2×
+2× +3×
+3× =
= …12分
…12分
分析:(I)根据有关公式可得 =
= ,s乙2<s甲2,所以乙的成绩较稳定,因此派乙参赛比较合适.
,s乙2<s甲2,所以乙的成绩较稳定,因此派乙参赛比较合适.
(II) 记“乙同学在一次数学竞赛中成绩高于80分”为事件A,则P(A)=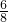 ,随机变量ξ 的可能取值为0、1、2、3,由题意可得ξ服从二项分布,即ξ~B(3,
,随机变量ξ 的可能取值为0、1、2、3,由题意可得ξ服从二项分布,即ξ~B(3, ),进而根据公式即可得到分布列与期望.
),进而根据公式即可得到分布列与期望.
点评:本题主要考查茎叶图、标准差与等可能事件的概率,以及离散型随机变量的分布列与期望.
 =
=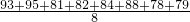 =85,
=85, =
=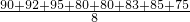 =85,
=85,所以s甲2=35.5,s乙2=41,
∴s甲2<s乙2,
∴乙的成绩较稳定,派乙参赛比较合适. …7分
(II) 记“乙同学在一次数学竞赛中成绩高于80分”为事件A,
则P(A)=
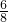 =
= .
.随机变量ξ 的可能取值为0、1、2、3,且ξ~B(3,
 ).
).∴P(ξ=k)=
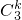 (
(  )k(
)k(  )3-k,k=0,1,2,3.
)3-k,k=0,1,2,3.所以变量ξ 的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =
= …12分
…12分分析:(I)根据有关公式可得
 =
= ,s乙2<s甲2,所以乙的成绩较稳定,因此派乙参赛比较合适.
,s乙2<s甲2,所以乙的成绩较稳定,因此派乙参赛比较合适. (II) 记“乙同学在一次数学竞赛中成绩高于80分”为事件A,则P(A)=
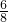 ,随机变量ξ 的可能取值为0、1、2、3,由题意可得ξ服从二项分布,即ξ~B(3,
,随机变量ξ 的可能取值为0、1、2、3,由题意可得ξ服从二项分布,即ξ~B(3, ),进而根据公式即可得到分布列与期望.
),进而根据公式即可得到分布列与期望.点评:本题主要考查茎叶图、标准差与等可能事件的概率,以及离散型随机变量的分布列与期望.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目

 ,
, (
( ,
, ,则a2等于
,则a2等于

