题目内容
已知命题p:椭圆的离心率e∈(0,1),命题q:与抛物线只有一个公共点的直线是此抛物线的切线,那么( )
分析:由椭圆的几何性质判断得命题p为真命题;根据平行于对称轴的直线与抛物线有一个交点,但不是抛物线的切线,判断q是假命题,由复合命题真值表逐个判断各个选项是否正确.
解答:解:由椭圆的几何性质判断:命题p为真命题;
∵与抛物线只有一个公共点的直线,除了抛物线的切线以外,还有平行于对称轴的直线,
∴命题q为假命题;
由复合命题真值表判断得:p∧q是假命题,故A错误;p∧(¬q)是真命题,故B正确;(¬p)∨q是假命题,故C正确;p∨q是真命题,故D错误;
故选B.
∵与抛物线只有一个公共点的直线,除了抛物线的切线以外,还有平行于对称轴的直线,
∴命题q为假命题;
由复合命题真值表判断得:p∧q是假命题,故A错误;p∧(¬q)是真命题,故B正确;(¬p)∨q是假命题,故C正确;p∨q是真命题,故D错误;
故选B.
点评:本题考查了椭圆的几何性质及直线与抛物线的位置关系,关键是利用抛物线中,平行于对称轴的直线与抛物线有一个交点,但不是抛物线的切线,来判断命题q为假命题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
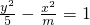 的离心率
的离心率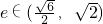 ,命题q:方程
,命题q:方程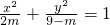 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.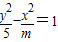 的离心率
的离心率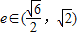 ,命题q:方程
,命题q:方程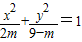 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.