题目内容
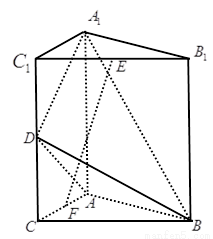
如图,直三棱柱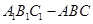 中,
中,
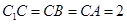 ,
,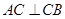 .
. 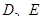 分别为棱
分别为棱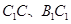 的中点.
的中点.
(1)求二面角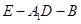 的平面角的余弦值;
的平面角的余弦值;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得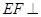 平
平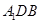 ?
?
若存在,确定其位置;若不存在,说明理由.
【答案】
(1) ;(2)见解析.
;(2)见解析.
【解析】本试题主要是考查了立体几何中的二面角的求解,线面垂直的判定定理的运用。
解:(1)如图所示,以 为
为 轴,
轴, 为
为 轴,
轴, 为
为 轴建立空间直角坐标系,由
轴建立空间直角坐标系,由
 可得
可得 ,
, ,
, ,
, ,
, .
.

 ,
, ,
, 可得
可得 ,
, …………2分
…………2分
设平面 的法向量为
的法向量为
 ,
,
故可令 ,
, ,
, ,
, ,
,
可得 ,
, ,
,
设平面 的法向量为
的法向量为
 ,
,
故可令 ,∴
,∴ ,
,
即求二面角 的余弦值为
的余弦值为 ;
……………8分
;
……………8分
(2)假设存在点 ,坐标为
,坐标为 ,则
,则 ,
,
 平面
平面 得
得 ,即
,即 ,
,
∴

 即为
即为 中点. ……………14分
中点. ……………14分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

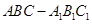 中,
中,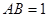 ,
,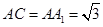 ,
,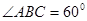 .
.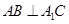 ;
;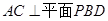
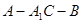 的正切值.
的正切值. 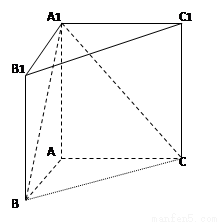
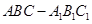 中,
中,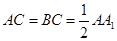 ,
,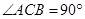 ,
,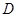 是棱
是棱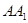 的中点.
的中点. ;
;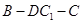 的余弦值。
的余弦值。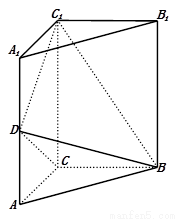
 中,
中,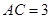 ,
,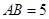 ,
,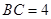
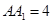 ,点
,点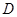 是
是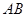 的中点.
的中点.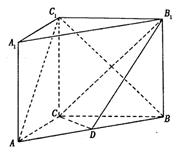
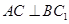 ;
;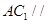 平面
平面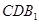 ;
;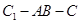 的正切值.
的正切值. 中,
中, ,
, ,点
,点 是
是 的中点,
的中点, ;
; ;
; 与平面
与平面 所成角的正切值.
所成角的正切值.