题目内容
若f（x）是奇函数，g（x）是偶函数，且f（x）+g（x）=
，则f（x）=________．
分析：由f（x）+g（x）=
，知
，由f（x）是奇函数，g（x）是偶函数，知
，由此能求出f（x）．解答：∵f（x）+g（x）=
，①∴
，∵f（x）是奇函数，g（x）是偶函数，
∴
，②①+②，得
=
，∴
．∴
=
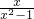．故答案为：
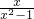．点评：本题考查函数的奇偶性的性质和应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
若f（x）是奇函数，且在（0，+∞）上是增函数，且f（-3）=0，则x•f（x）＜0的解是（ ）
| A、（-3，0）∪（3，+∞） | B、（-∞，-3）∪（0，3） | C、（-∞，-3）∪（3，+∞） | D、（-3，0）∪（0，3） |