题目内容
数列{an}满足a1=1,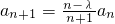 ,其中λ∈R,n=1,2,….给出下列命题:
,其中λ∈R,n=1,2,….给出下列命题:
①?λ∈R,对于任意i∈N*,ai>0;
②?λ∈R,对于任意i≥2(i∈N*),aiai+1<0;
③?λ∈R,m∈N*,当i>m(i∈N*)时总有ai<0.
其中正确的命题是________.(写出所有正确命题的序号)
①③
分析:①:当λ≤0时, ,an>0,从而可得
,an>0,从而可得
②:由 可得λ>i,从而可得
可得λ>i,从而可得
③:设λ=3.1, ,
, ,
, ,
,
当i>4时, ,从而有a5<0,a6<0,…ai<0,,从而可得
,从而有a5<0,a6<0,…ai<0,,从而可得
解答:①:当λ≤0时, ,an>0,故①正确
,an>0,故①正确
②:由 可得λ>i,从而可得λ为变量,故②错误
可得λ>i,从而可得λ为变量,故②错误
③:设λ=3.1, ,
, ,
, ,
,
当i>4时, ,从而有a5<0,a6<0,…ai<0,故③正确
,从而有a5<0,a6<0,…ai<0,故③正确
故答案为:①③
点评:本题主要考查了利用数列的递推公式判断数列中的项满足的条件,解题的关键是要能够灵活利用数列的综合知识.
分析:①:当λ≤0时,
 ,an>0,从而可得
,an>0,从而可得②:由
 可得λ>i,从而可得
可得λ>i,从而可得③:设λ=3.1,
 ,
, ,
, ,
,当i>4时,
 ,从而有a5<0,a6<0,…ai<0,,从而可得
,从而有a5<0,a6<0,…ai<0,,从而可得解答:①:当λ≤0时,
 ,an>0,故①正确
,an>0,故①正确②:由
 可得λ>i,从而可得λ为变量,故②错误
可得λ>i,从而可得λ为变量,故②错误③:设λ=3.1,
 ,
, ,
, ,
,当i>4时,
 ,从而有a5<0,a6<0,…ai<0,故③正确
,从而有a5<0,a6<0,…ai<0,故③正确故答案为:①③
点评:本题主要考查了利用数列的递推公式判断数列中的项满足的条件,解题的关键是要能够灵活利用数列的综合知识.

练习册系列答案
相关题目