题目内容
已知a,b,c均为正数,且 ,
, ,
, ,则a,b,c的大小关系为
,则a,b,c的大小关系为
- A.c<a<b
- B.a<b<c
- C.c<b<a
- D.b<a<c
C
分析:由三个方程 ,
, ,
, ,判断出a,b,c的取值范围,再比较它们的大小关系选出正确选项
,判断出a,b,c的取值范围,再比较它们的大小关系选出正确选项
解答:∵a,b,c均为正数,且 ,
, ,
, ,
,
∴ >0,得a>1,从而
>0,得a>1,从而 ,即log2a<1,由此得1<a<2
,即log2a<1,由此得1<a<2
 >0,得0<b<1,从而有
>0,得0<b<1,从而有 ,可得
,可得 <b<1
<b<1
 >0,得0<c<1,从而有
>0,得0<c<1,从而有 >1,可得0<c<
>1,可得0<c<
∴c<b<a
故选C
点评:本题考查不等式比较大小,熟练掌握指数函数与对数函数的性质是解本题的关键,本题采用了中间量法比较三个数的大小,此法特点是根据有关知识求出三个数具体范围,从而得出三数的大小.本题对推理判断的能力要求较高,是一个能力型的题.
分析:由三个方程
 ,
, ,
, ,判断出a,b,c的取值范围,再比较它们的大小关系选出正确选项
,判断出a,b,c的取值范围,再比较它们的大小关系选出正确选项解答:∵a,b,c均为正数,且
 ,
, ,
, ,
,∴
 >0,得a>1,从而
>0,得a>1,从而 ,即log2a<1,由此得1<a<2
,即log2a<1,由此得1<a<2 >0,得0<b<1,从而有
>0,得0<b<1,从而有 ,可得
,可得 <b<1
<b<1 >0,得0<c<1,从而有
>0,得0<c<1,从而有 >1,可得0<c<
>1,可得0<c<
∴c<b<a
故选C
点评:本题考查不等式比较大小,熟练掌握指数函数与对数函数的性质是解本题的关键,本题采用了中间量法比较三个数的大小,此法特点是根据有关知识求出三个数具体范围,从而得出三数的大小.本题对推理判断的能力要求较高,是一个能力型的题.

练习册系列答案
相关题目
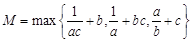 ,则M的最小值为 .
,则M的最小值为 .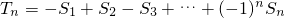 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;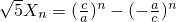 (n∈N+),证明:数列{
(n∈N+),证明:数列{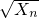 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.