题目内容

椭圆的焦点在x轴上，长轴长是短轴长的2倍，则a=    ．
【答案】分析：利用椭圆的标准方程及其性质即可得出．
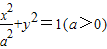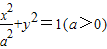解答：解：由椭圆的焦点在x轴上，∴a＞1=b，
由题意可得2a=2×2×1，解得a=2．
故答案为2．
点评：熟练掌握椭圆的标准方程及其性质是解题的关键．
练习册系列答案
相关题目
已知椭圆的顶点与双曲线
y2
4
-
x2
12
=1的焦点重合，它们的离心率之和为
13
5
，若椭圆的焦点在x轴上，求椭圆的标准方程．
一个椭圆长轴的长度、短轴的长度和焦距成等差数列，（1）求椭圆的离心率；（2）若椭圆的焦点在x轴上且短轴长为8，求椭圆的标准方程．
求满足下列条件的椭圆的标准方程．
（1）已知椭圆的焦点在X轴上，长轴长是短轴长的3倍，且过点A（3，0）．
（2）已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P1(
6
，1)，P2(-
3
，-
2
)．
己知椭圆的焦点在x轴上，它的一个焦点与抛物线x2=4y的焦点之间的距离为
5
，离心率e=
2
5
5
，过椭圆的左焦点厂做一条与坐标轴不垂直的直线L交椭圆于A，B两点．
（1）求椭圆的标准方程；
（2）设点M（m，0）是线段OF1上的一个动点，且（
MA
+
MB
）⊥
AB
，求m的取值范围．
（2012•宝鸡模拟）平面内点P与两定点A1（-a，0），A2（a，0）（其中a＞0）连线的斜率之积为非零常数m，已知点P的轨迹是椭圆C，离心率是
2
2
．
（1）求m的值；
（2）设椭圆的焦点在x轴上，若过点（2，3）且斜率为-1的直线被椭圆C所截线段的长度为
20
3
3
，求此椭圆的焦点坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网