题目内容
在下列四个命题中,把你认为正确的命题的序号都填在横线上________.
①函数 的定义域是
的定义域是 ;
;
②已知 ,且α∈[0,2π],则α的取值集合是
,且α∈[0,2π],则α的取值集合是 ;
;
③函数f(x)=sin2x+cos2x图象的最大值为 ;
;
④函数y=cos2x+sinx的最小值为-1.
①③④
分析:①根据正切函数的定义可知定义域为x+ ≠kπ+
≠kπ+ 解出x的范围即可判断;
解出x的范围即可判断;
②因为sinα= ,且α∈[0,2π],根据特殊角的三角函数值可得α的值即可判断;
,且α∈[0,2π],根据特殊角的三角函数值可得α的值即可判断;
③由函数关于直线x=- 对称得到f(0)=f(-
对称得到f(0)=f(- ),代入求出a即可判断;
),代入求出a即可判断;
④利用同角三角函数间的基本关系化简y,并利用二次函数求最值的方法得到y的最小值即可判断.
解答:根据正切函数的定义得: 故①正确;
故①正确;
由 ,且
,且  或
或 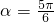 ,故②不正确;
,故②不正确;
函数f(x)的图象关于直线 对称?
对称? ,故③正确;
,故③正确; ,
, 故④正确.
故④正确.
所以正确的序号有:①③④
故答案为:①③④
点评:本题考查学生知识比较多,考查了正切函数的定义域,特殊角的三角函数值,以及正弦函数的对称性,利用同角三角函数间的基本关系化简求值,二次函数求最值的方法.
分析:①根据正切函数的定义可知定义域为x+
 ≠kπ+
≠kπ+ 解出x的范围即可判断;
解出x的范围即可判断;②因为sinα=
 ,且α∈[0,2π],根据特殊角的三角函数值可得α的值即可判断;
,且α∈[0,2π],根据特殊角的三角函数值可得α的值即可判断;③由函数关于直线x=-
 对称得到f(0)=f(-
对称得到f(0)=f(- ),代入求出a即可判断;
),代入求出a即可判断;④利用同角三角函数间的基本关系化简y,并利用二次函数求最值的方法得到y的最小值即可判断.
解答:根据正切函数的定义得:
 故①正确;
故①正确;由
 ,且
,且  或
或 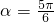 ,故②不正确;
,故②不正确;函数f(x)的图象关于直线
 对称?
对称? ,故③正确;
,故③正确; ,
, 故④正确.
故④正确.所以正确的序号有:①③④
故答案为:①③④
点评:本题考查学生知识比较多,考查了正切函数的定义域,特殊角的三角函数值,以及正弦函数的对称性,利用同角三角函数间的基本关系化简求值,二次函数求最值的方法.

练习册系列答案
相关题目
 的定义域是
的定义域是 ;
; ,且α∈[0,2π],则α的取值集合是
,且α∈[0,2π],则α的取值集合是 ;
; ;
;