题目内容
己知函数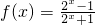 ,
,
(Ⅰ)证明函数f(x)是R上的增函数;
(Ⅱ)求函数f(x)的值域.
(Ⅲ)令 .判定函数g(x)的奇偶性,并证明.
.判定函数g(x)的奇偶性,并证明.
解:(Ⅰ)设x,x是R内任意两个值,且x1<x2,则x2-x1>0
y2-y1=f(x2)-f(x1)= -
-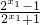
= =
=
当x1<x2时, <
<
∴ -
- >0.又
>0.又 +1>0,
+1>0, +1>0
+1>0
∴y2-y1>0
∴f(x)是R上的增函数.
(Ⅱ):(1)∵ ,又2x>0,
,又2x>0,
∴-1<y<1
函数f(x)的值域为(-1,1);
(Ⅲ)由题意知g(x)= •
•
易知函数g(x)的定义域为(-∞,0)∪(0,+∞)
g(-x)= •
• =
= •
• =-
=- •
• =-g(x)
=-g(x)
∴函数g(x)为奇函数.
分析:(Ⅰ)先对函数作适当变形,再利用定义证明,先在定义域上任取两个变量,且界定大小,再作差变形,与零比较,由定义得到结论.
(Ⅱ)利用有界法求解,将函数看作方程,解得 ,再由2x>0,解得y的范围,即为所求.
,再由2x>0,解得y的范围,即为所求.
(Ⅲ)求出函数g(x)的定义域,利用函数奇偶性的定义加以判断即可得到结论.
点评:本题主要考查函数奇偶性、值域的求法和单调性的证明,值域常见方法有单调性法,基本函数法,有界性法,判别式法等,证明单调性一般有定义法,导数法,考查运算能力以及分析问题解决问题的能力.属中档题.
y2-y1=f(x2)-f(x1)=
 -
-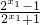
=
 =
=
当x1<x2时,
 <
<
∴
 -
- >0.又
>0.又 +1>0,
+1>0, +1>0
+1>0∴y2-y1>0
∴f(x)是R上的增函数.
(Ⅱ):(1)∵
 ,又2x>0,
,又2x>0,∴-1<y<1
函数f(x)的值域为(-1,1);
(Ⅲ)由题意知g(x)=
 •
•
易知函数g(x)的定义域为(-∞,0)∪(0,+∞)
g(-x)=
 •
• =
= •
• =-
=- •
• =-g(x)
=-g(x)∴函数g(x)为奇函数.
分析:(Ⅰ)先对函数作适当变形,再利用定义证明,先在定义域上任取两个变量,且界定大小,再作差变形,与零比较,由定义得到结论.
(Ⅱ)利用有界法求解,将函数看作方程,解得
 ,再由2x>0,解得y的范围,即为所求.
,再由2x>0,解得y的范围,即为所求.(Ⅲ)求出函数g(x)的定义域,利用函数奇偶性的定义加以判断即可得到结论.
点评:本题主要考查函数奇偶性、值域的求法和单调性的证明,值域常见方法有单调性法,基本函数法,有界性法,判别式法等,证明单调性一般有定义法,导数法,考查运算能力以及分析问题解决问题的能力.属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目