题目内容

已知P为棱长为1的正方体ABCD-A1B1C1D1内（含正方体表面）任意一点，则
AP
•
AC
的最大值为
2
2
．
分析：写出数量积的表达式，利用向量的投影，判断P的位置，然后求出数量积的最大值．
解答：解：由题意画出图形如图，
因为
AP
•
AC
=|
AP
||
AC
|cos＜
AP
，
AC
＞，
|
AP
| cos＜
AP
，
AC
＞是向量
AP
在
AC
上的投影，
所以当P在C1位置时，投影最大，
AP
•
AC
的最大值为：
AC
2=(
12+12
)2=2．
故答案为：2．
点评：本题考查向量的数量积，向量的投影，表达式的几何意义，考查计算能力．
练习册系列答案
相关题目
已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6，侧棱长AA1=2
7
，它的外接球的球心为O，
点E是AB的中点，点P是球O的球面上任意一点，有以下判断：
（1）PE长的最大值是9；
（2）P到平面EBC的距离最大值是4+
7
；
（3）存在过点E的平面截球O的截面面积是3π；
（4）三棱锥P-AEC1体积的最大值是20．
其中正确判断的序号是
 
．
已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6，侧棱长AA1=2
7
，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断，
（1）PE长的最大值是9；（2）三棱锥P-EBC的最大值是
32
3
；（3）存在过点E的平面，截球O的截面面积是3π；（4）三棱锥P-AEC1体积的最大值是20．
正确的是
 
．
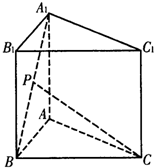已知正三棱柱ABC-A1B1C的各条棱长都为a，P为A1B上的点，且PC⊥AB
（1）求二面角P-AC-B的正切值；
（2）求点B到平面PAC的距离．
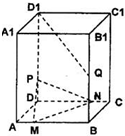已知正四棱柱ABCD-A1B1C1D1的底面边长为4，侧棱长为6，Q为BB1的中点，P∈DD1，M∈AB，N∈CD且AM=1，DN=3，（I）若PD=
32
，证明：（I）D1Q∥面PMN；
（II）若P为DD1的中点，求面PMN与面AA1D1D所成二面角的大小；
（III）在（II）的条件下，求点Q到面PMN的距离．
已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6，侧棱长AA1=2
7
，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断，
（1）PE长的最大值是9；（2）三棱锥P-EBC的最大值是
32
3
；（3）存在过点E的平面，截球O的截面面积是3π；（4）三棱锥P-AEC1体积的最大值是20．
正确的是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网