题目内容
【题目】四边形![]() 的顶点
的顶点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(![]() )此四边形是否有外接圆,若有,求出外接圆的方程;若没有,请说明理由.
)此四边形是否有外接圆,若有,求出外接圆的方程;若没有,请说明理由.
(![]() )记
)记![]() 的外接圆为
的外接圆为![]() ,过
,过![]() 上的点
上的点![]() 作圆
作圆![]() 的切线
的切线![]() ,设与
,设与![]() 轴、
轴、![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 、
、![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(![]() )外接圆方程为
)外接圆方程为![]() (
(![]() )
)![]()
【解析】试题分析:
(1)先求出过![]() 三点的圆,通过验证点D是否在此圆上来判断四边形是否有外接圆。(2)由(1)得
三点的圆,通过验证点D是否在此圆上来判断四边形是否有外接圆。(2)由(1)得![]() 的外接圆为
的外接圆为![]() 的方程为
的方程为![]() ,先求得
,先求得![]() ,可得切线
,可得切线![]() 的斜率
的斜率![]() ,切线方程为
,切线方程为![]() ,整理得切线
,整理得切线![]() ,然后求得点
,然后求得点![]() 的坐标,求得
的坐标,求得![]() ,根据基本不等式可得
,根据基本不等式可得![]() ,即为所求。
,即为所求。
试题解析:
(![]() )设过
)设过![]() 三点的外接圆为
三点的外接圆为![]() ,圆心
,圆心![]() ,半径为
,半径为![]() ,
,
则圆![]() 的标准方程为
的标准方程为![]() ,
,
由题意得 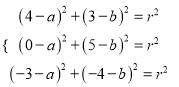 ,解得
,解得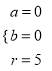
∴ 圆![]() ,
,
验证可得点![]() 在圆
在圆![]() 上。
上。
∴ 四边形![]() 有外接圆,其方程为
有外接圆,其方程为![]() .
.
(![]() )由(1)得
)由(1)得![]() 的外接圆为
的外接圆为![]() 的方程为
的方程为![]() 。
。
由题意得![]() ,
,
∴ 切线![]() 的斜率
的斜率![]() ,从而切线
,从而切线![]() 的方程为
的方程为![]() ,
,
整理得![]() ,
,
又点![]() 在圆
在圆![]() 上,故
上,故![]() ,
,
∴ 切线![]() ,
,
令![]() ,得
,得![]() ,∴
,∴ 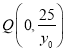 ,
,
令![]() ,得
,得![]() ,∴
,∴ 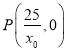 ,
,
∴ ![]() 面积
面积![]() ,
,
∵ ![]() ,
,
∴ ![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
即![]() 面积的最小值为
面积的最小值为![]() ,此时点
,此时点![]() .
.

练习册系列答案
相关题目