题目内容
如图,已知正方形 的边长为
的边长为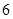 ,点
,点 分别在边
分别在边 上,
上, ,现将△
,现将△ 沿线段
沿线段 折起到△
折起到△ 位置,使得
位置,使得 .
.
(1)求五棱锥 的体积;
的体积;
(2)求平面 与平面
与平面 的夹角.
的夹角.
(1)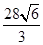 ;(2)
;(2)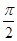
解析试题分析:(1)由于△ 沿线段
沿线段 折起到△
折起到△ 的过程中,平面
的过程中,平面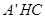
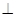 平面
平面 始终成立.所以
始终成立.所以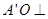 平面
平面 .又因为
.又因为 ,正方形
,正方形 的边长为
的边长为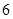 ,点
,点 分别在边
分别在边 上,
上, .即可求得结论.
.即可求得结论.
(2)依题已建立空间直角坐标系.求出两个平面的法向量,由法向量的夹角得到平面 与平面
与平面 的夹角.
的夹角.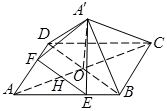
试题解析:(1)连接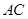 ,设
,设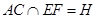 ,由
,由 是正方形,
是正方形, ,
,
得 是
是 的中点,且
的中点,且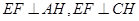 ,从而有
,从而有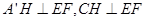 ,
,
所以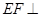 平面
平面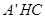 ,从而平面
,从而平面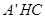
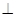 平面
平面 , 2分
, 2分
过点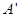 作
作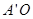 垂直
垂直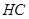 且与
且与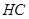 相交于点
相交于点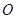 ,
,
则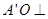 平面
平面 4分
4分
因为正方形 的边长为
的边长为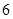 ,
, ,
,
得到: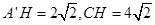 ,
,
所以 ,
,
所以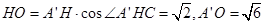
所以五棱锥 的体积
的体积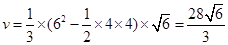 ; 6分
; 6分
(2)由(1)知道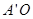
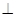 平面
平面 ,且
,且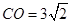 ,即点
,即点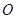 是
是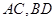 的交点,
的交点,
如图以点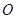 为原点,
为原点,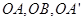 所在直线分别为
所在直线分别为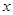 轴,
轴,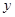 轴,
轴,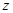 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则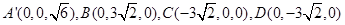 ,
,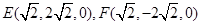 7分
7分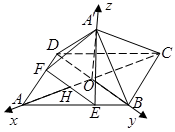
设平面 的法向量为
的法向量为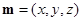 ,则
,则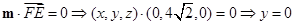 ,
,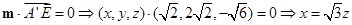 ,
,
令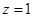 ,则
,则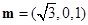 , 9分
, 9分
设平面 的法向量
的法向量
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
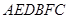 的直观图及三视图如图所示,
的直观图及三视图如图所示,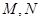 分别为
分别为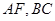 的中点.
的中点.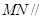 平面
平面 ;
; 的体积.
的体积.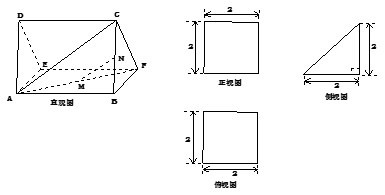
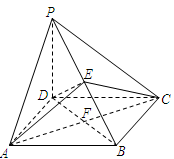
 中,
中, 底面
底面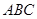 ,
,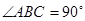 ,且
,且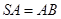 ,
,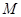 是
是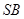 的中点,
的中点,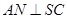 且交
且交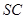 于点
于点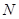 .
.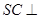 平面
平面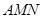 ;
;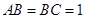 时,求三棱锥
时,求三棱锥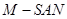 的体积.
的体积.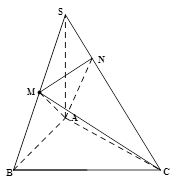
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
,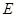 为棱
为棱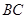 的中点,求
的中点,求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);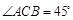 ,
,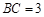 ,过动点A作
,过动点A作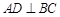 ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿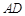 将△
将△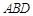 折起,使
折起,使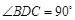 (如图2所示).
(如图2所示).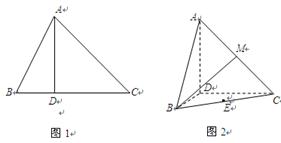
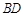 的长为多少时,三棱锥
的长为多少时,三棱锥 的体积最大;
的体积最大;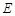 ,
,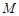 分别为棱
分别为棱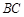 ,
,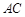 的中点,试在棱
的中点,试在棱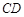 上确定一点
上确定一点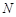 ,使得
,使得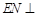
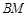 ,并求
,并求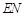 与平面
与平面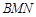 所成角的大小.
所成角的大小.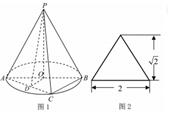
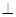 平面POD;
平面POD;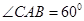 ,在三棱锥A-PBC中,求点A到平面PBC的距离.
,在三棱锥A-PBC中,求点A到平面PBC的距离. 中,
中,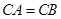 ,
,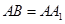 ,
,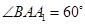 .
.
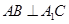 ;
;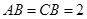 ,
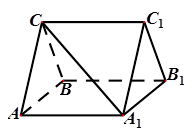
,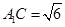 ,求三棱柱
,求三棱柱 A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
 ,求三棱柱ABC
,求三棱柱ABC