题目内容
点B是双曲线 上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为( )
上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为( )A.

B.3
C.

D.2
【答案】分析:由已知中点B是双曲线 上在第一象限的任意一点,不妨取特殊的点,通过构造直角三角形,利用直角三角形中几何元素,沟通a,b,c的关系,即可求出该双曲线的离心率.
上在第一象限的任意一点,不妨取特殊的点,通过构造直角三角形,利用直角三角形中几何元素,沟通a,b,c的关系,即可求出该双曲线的离心率.
解答: 解:∵点B是双曲线
解:∵点B是双曲线 上在第一象限的任意一点,不妨取过F作x轴的垂线交双曲线
上在第一象限的任意一点,不妨取过F作x轴的垂线交双曲线 在第一象限内的交点为B.如图.
在第一象限内的交点为B.如图.
由题意得,在直角三角形ABF中,BF= ,AF=a+c,∠BAF=45°,
,AF=a+c,∠BAF=45°,
∴ =a+c,即b2=a2+ac,⇒c2-a2=a2+ac
=a+c,即b2=a2+ac,⇒c2-a2=a2+ac
解得e= =2.
=2.
故选D.
点评:本题考查的知识点是双曲线的简单性质,双曲线的渐近线与离心率存在对应关系,通过a,b,c的比例关系可以求离心率.
 上在第一象限的任意一点,不妨取特殊的点,通过构造直角三角形,利用直角三角形中几何元素,沟通a,b,c的关系,即可求出该双曲线的离心率.
上在第一象限的任意一点,不妨取特殊的点,通过构造直角三角形,利用直角三角形中几何元素,沟通a,b,c的关系,即可求出该双曲线的离心率.解答:
 解:∵点B是双曲线
解:∵点B是双曲线 上在第一象限的任意一点,不妨取过F作x轴的垂线交双曲线
上在第一象限的任意一点,不妨取过F作x轴的垂线交双曲线 在第一象限内的交点为B.如图.
在第一象限内的交点为B.如图.由题意得,在直角三角形ABF中,BF=
 ,AF=a+c,∠BAF=45°,
,AF=a+c,∠BAF=45°,∴
 =a+c,即b2=a2+ac,⇒c2-a2=a2+ac
=a+c,即b2=a2+ac,⇒c2-a2=a2+ac解得e=
 =2.
=2.故选D.
点评:本题考查的知识点是双曲线的简单性质,双曲线的渐近线与离心率存在对应关系,通过a,b,c的比例关系可以求离心率.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
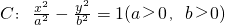 上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为
上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为

 上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为( )
上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为( )

 上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为( )
上在第一象限的任意一点,A为双曲线的左顶点,F为右焦点,若∠BFA=2∠BAF,则双曲线C的离心率为( )
