题目内容
已知直线 的方程为
的方程为 ,圆
,圆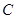 的方程为
的方程为 .
.
(1) 把直线 和圆
和圆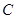 的方程化为普通方程;
的方程化为普通方程;
(2) 求圆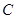 上的点到直线
上的点到直线 距离的最大值.
距离的最大值.
 的方程为
的方程为 ,圆
,圆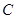 的方程为
的方程为 .
.(1) 把直线
 和圆
和圆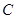 的方程化为普通方程;
的方程化为普通方程;(2) 求圆
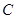 上的点到直线
上的点到直线 距离的最大值.
距离的最大值.(1) :
: ,
, :
: ;(2)
;(2) .
.
 :
: ,
, :
: ;(2)
;(2) .
.试题分析:(1)以极点为原点,极轴为
 轴正半轴建立直角坐标系,利用和角的正弦函数,即可求得该直线的直角坐标方程;利用三角函数的同角关系式中的平方关系,消去圆
轴正半轴建立直角坐标系,利用和角的正弦函数,即可求得该直线的直角坐标方程;利用三角函数的同角关系式中的平方关系,消去圆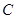 的参数方程中的参数,即可得圆
的参数方程中的参数,即可得圆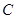 的普通方程为;(2)求出圆心
的普通方程为;(2)求出圆心 到直线
到直线 的距离,即可得到圆
的距离,即可得到圆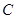 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.(1)直线
 的方程为
的方程为 .
. 圆
 的方程为
的方程为 .
. (2) 易求得圆心
 到直线
到直线 的距离为
的距离为 ,
,所以距离的最大值为
 =
= .
. 
练习册系列答案
相关题目
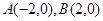 ,点
,点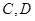 依次满足
依次满足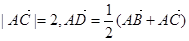 。
。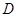 的轨迹;
的轨迹; 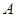 作直线
作直线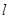 交以
交以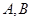 为焦点的椭圆于
为焦点的椭圆于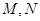 两点,线段
两点,线段 的中点到
的中点到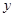 轴的距离为
轴的距离为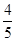 ,且直线
,且直线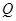 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点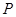 及以
及以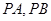 都相切,如存在,求出
都相切,如存在,求出 分别为椭圆
分别为椭圆 的左、右焦点,斜率为
的左、右焦点,斜率为 的直线
的直线 经过右焦点
经过右焦点 ,且与椭圆W相交于
,且与椭圆W相交于 两点.
两点.  的周长;
的周长;  ;
; ,它的中心为M
,它的中心为M ,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.
,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积. ,则动点P的轨迹方程是( )
,则动点P的轨迹方程是( )



 与圆
与圆 交于
交于 两点,则与向量
两点,则与向量 (
( 为坐标原点)共线的一个向量为()
为坐标原点)共线的一个向量为()


