题目内容
 如图所示,ABCD是正方形,PA⊥平面ABCD,E、F是AC、PC的中点
如图所示,ABCD是正方形,PA⊥平面ABCD,E、F是AC、PC的中点(1)求证:AC⊥DF;
(2)若PA=2,AB=1,求三棱锥C-PED的体积.
分析:(1)连接ED、EF,由E、F是AC、PC的中点,可得EF∥PA,再由PA⊥平面ABCD,可得EF⊥平面ABCD,进而EF⊥AC,由底面的对角线互相垂直及线面垂直的判定定理可得:AC⊥平面DEF,进而AC⊥DF;
(2)由已知可得PA为三棱锥P-CED的高,由PA=2,AB=1,求出棱锥的底面和高,代入可得答案.
(2)由已知可得PA为三棱锥P-CED的高,由PA=2,AB=1,求出棱锥的底面和高,代入可得答案.
解答:证明:(1)连接ED、EF,
∵ABCD是正方形,E是AC的中点,
∴ED⊥AC…(1分)
又∵E、F分别是AC、PC的中点
∴EF∥PA…(2分)
又∵PA⊥平面ABCD,
∴EF⊥平面ABCD,…(3分)
∵AC?平面ABCD,
∴EF⊥AC…(4分)
又∵ED∩EF=E,ED,EF?平面DEF
∴AC⊥平面DEF…(5分)
又∵DF?平面DEF
故AC⊥DF…(7分)
解:(2)∵PA⊥平面ABCD,
∴是PA三棱锥P-CED的高,且PA=2
∵ABCD是正方形,E是AC的中点,
∴△CED是等腰直角三角形…(9分)
又∵AB=1,
故CE=ED=
,
S△CED=
CE•ED=
•
•
=
…(12分)
故VC-PED=VP-CED=
•S△CED•PA=
•
•2=
…(14分)
∵ABCD是正方形,E是AC的中点,
∴ED⊥AC…(1分)
又∵E、F分别是AC、PC的中点
∴EF∥PA…(2分)
又∵PA⊥平面ABCD,
∴EF⊥平面ABCD,…(3分)
∵AC?平面ABCD,
∴EF⊥AC…(4分)
又∵ED∩EF=E,ED,EF?平面DEF
∴AC⊥平面DEF…(5分)
又∵DF?平面DEF
故AC⊥DF…(7分)
解:(2)∵PA⊥平面ABCD,
∴是PA三棱锥P-CED的高,且PA=2
∵ABCD是正方形,E是AC的中点,
∴△CED是等腰直角三角形…(9分)
又∵AB=1,
故CE=ED=
| ||
| 2 |
S△CED=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
故VC-PED=VP-CED=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
点评:本题考查的知识点是线面垂直的判定与性质,棱锥的体积,熟练掌握空间线面垂直与线线垂直的互相转化是解答的关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
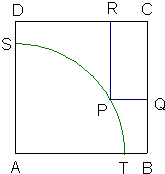 如图所示,ABCD是一块边长为100米的正方形地皮,其中ATPS是一个半径为90米的扇形小山,P是弧TS上一点,其余都是平地.现要在平地上建造矩形停车场PQCR,求停车场PQCR的最大面积.
如图所示,ABCD是一块边长为100米的正方形地皮,其中ATPS是一个半径为90米的扇形小山,P是弧TS上一点,其余都是平地.现要在平地上建造矩形停车场PQCR,求停车场PQCR的最大面积.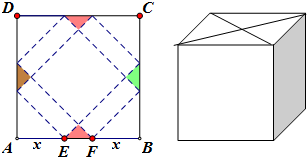 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 11、如图所示,ABCD是一个平面图形的斜二侧直观图,则该图形是( )
11、如图所示,ABCD是一个平面图形的斜二侧直观图,则该图形是( ) 如图所示,ABCD是一平面图形的水平放置的斜二侧直观图.在斜二侧直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行.若AB=6,AD=2,则这个平面图形的实际面积为( )
如图所示,ABCD是一平面图形的水平放置的斜二侧直观图.在斜二侧直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行.若AB=6,AD=2,则这个平面图形的实际面积为( )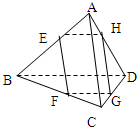 如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,AC=m,BD=n,则四 边形EFGH的面积为
如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,AC=m,BD=n,则四 边形EFGH的面积为