Question

10．某研究机构对高三学生的记忆力x和判断力y进行统计分析，所得数据如表所示：

x	6	8	10	12
y	2	3	5	6

（1）在给定的坐标系中画出表中数据的散点图；
（2）试根据最小二乘法原理，求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并在给定的坐标系中画出回归直线；
（3）试根据（2）求出的线性回归方程，预测记忆力为9的学生的判断力．
参考公式：用最小二乘法求线性回归方程系数公式：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}，\hat a=\overline y-\hat b\overline x$．

Answer 1

分析 （1）根据所给的这一组数据，得到4个点的坐标，把这几个点的坐标在直角坐标系中描出对应的点，得到散点图，从散点图可以看出，这两个两之间是正相关．
（2）根据所给的这组数据，写出利用最小二乘法要用的量的结果，把所求的这些结果代入公式求出线性回归方程的系数，进而求出a的值，写出线性回归方程．
（3）根据上一问做出的线性回归方程，把x=9的值代入方程，估计出对应的y的值．

解答 解：（1）散点图如图所示．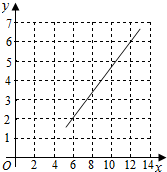
…（1分）
（2）$\overline x=\frac{6+8+10+12}{4}=9$，$\overline y=\frac{2+3+5+6}{4}=4$…（3分）
$\sum_{i=1}^4{{x_i}{y_i}}=6×2+8×3+10×5+12×6=158$…（4分）
$\sum_{i=1}^4{{x_i}^2}={6^2}+{8^2}+{10^2}+{12^2}=344$…（5分）
$\hat b=\frac{{\sum_{i=1}^4{{x_i}{y_i}}-4\overline x\overline y}}{{\sum_{i=1}^4{{x_i}^2}-4{{\overline x}^2}}}=\frac{158-4×9×4}{{344-4×{9^2}}}=0.7$…（7分）
$\hat a=\overline y-\hat b\overline x=4-0.7×9=-2.3$…（8分）
故线性回归方程为$\hat y=0.7x-2.3$．…（9分）
画出回归方程…（10分）
（3）由题意，该同学的记忆力为9，则预测他的判断力为：$\hat y=0.7×9-2.3=4$…（11分）
预测这位同学的判断力约为4．…（12分）

点评 本题考查线性回归方程的求法和应用，是一个基础题，这种题目解题的关键是求出最小二乘法所要用到的量，数字的运算不要出错．