题目内容
已知A(5,2a-1),B(a+1,a-4),当|AB|取最小值时,实数a的值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
分析:首先根据两点之间的距离公式写出两点之间的距离,得到一个被开方数是一个关于a的二次函数的形式,对于二次函数配方整理,得到当a取
时,|AB|取到最小值.
| 1 |
| 2 |
解答:解:|AB|=
=
=
,
当a=
时,|AB|取最小值.
故选D.
| (a+1-5)2+(a-4-2a+1)2 |
| a2-8a+16+a2+6a+9 |
=
2(a-
|
当a=
| 1 |
| 2 |
故选D.
点评:本题考查平面上两点间距离公式的应用和二次函数求最值的方法.平面上两点间的距离公式是解析几何的一个必考的公式,必须熟练掌握,这是一个综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
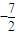



 =(b,c-2a),
=(b,c-2a), =(cosC,cosB),且
=(cosC,cosB),且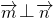
 ,求△ABC的面积.
,求△ABC的面积.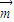 =(b,c-2a),
=(b,c-2a),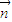 =(cosC,cosB),且
=(cosC,cosB),且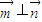
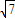 ,求△ABC的面积.
,求△ABC的面积.