题目内容
已知函数
的定义域是集合A，函数 g（x）=lg[x2﹣（2a+1）x+a2+a]的定义域是集合B．
（1）当a=1时，求集合A、B；
（2）若A∩B=A，求实数a的取值范围．
的定义域是集合A，函数 g（x）=lg[x2﹣（2a+1）x+a2+a]的定义域是集合B．（1）当a=1时，求集合A、B；
（2）若A∩B=A，求实数a的取值范围．
解：（1）由题意（x+1）（x﹣2）≥0所以 A={x|x≤﹣1或x≥2}；
x2﹣（2a+1）x+a2+a＞0 B={x|x＜a或x＞a+1}；
∵当a=1时
∴B={x|x＜1或x＞2}
（2）由（1）知 A={x|x≤﹣1或x≥2}；
B={x|x＜a或x＞a+1}；
由A∩B=A
得A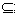
B，
因此 a＞﹣1且a+1≤2
解得：﹣1＜a≤1，
∴实数a的取值范围是（﹣1，1]．
x2﹣（2a+1）x+a2+a＞0 B={x|x＜a或x＞a+1}；
∵当a=1时
∴B={x|x＜1或x＞2}
（2）由（1）知 A={x|x≤﹣1或x≥2}；
B={x|x＜a或x＞a+1}；
由A∩B=A
得A
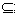B，因此 a＞﹣1且a+1≤2
解得：﹣1＜a≤1，
∴实数a的取值范围是（﹣1，1]．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
的定义域为
。
（其中
）不是函数
图像的切线；
上单调性，并证明；
满足
，求关于
的不等式
的解集
的定义域为
。
（其中
）不是函数
图像的切线；
上单调性，并证明；
满足
，求关于
的不等式
的解集
的定义域是A, 函数
定义域B
的值域是
. 
的解集是A,求
的值. 
（R是实数集）.
的定义域关于原点对称，且满足以下三个条件：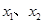
、
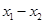是定义域中的数时，有
；
是定义域中的一个数）；
时，
．
与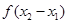
之间的关系，并推断函数
上的单调性，并证明；
时，
的值；②求不等式
的解集． 
的定义域为
，且
的图像如右图所示，记
，则不等式
的解集是 ▲ .