题目内容
已知复数 (
( ),
), 是实数,
是实数, 是虚数单位.
是虚数单位.
(1)求复数z;
(2)若复数 所表示的点在第一象限,求实数m的取值范围.
所表示的点在第一象限,求实数m的取值范围.
(1) .
.
(2)  时,复数
时,复数 所表示的点在第一象限.
所表示的点在第一象限.
解析试题分析:(1)




 .
. 
又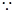
 是实数,
是实数, ,
, 
 ,即
,即 .
. 
(2) 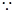
 ,
, ,
,
 ,
, 
又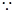 复数
复数 所表示的点在第一象限,
所表示的点在第一象限,

解得 ,即
,即 时,复数
时,复数 所表示的点在第一象限.
所表示的点在第一象限. 
考点:复数的相等,复数的代数运算,复数的几何意义。
点评:中档题,复数的除法,通过分子分母同乘分母的共轭复数,实现“分母实数化”。

练习册系列答案
相关题目
 满足:
满足: 且
且 是纯虚数,求复数
是纯虚数,求复数 为复数,且
为复数,且 (
( 为虚数单位),求
为虚数单位),求 (
( 为虚数单位)无解.
为虚数单位)无解. 是
是 =4+2i,求复数z.
=4+2i,求复数z. 满足
满足 ,且
,且 在复平面上对应的点在第二、四象限的角平分线上,
在复平面上对应的点在第二、四象限的角平分线上, ,求
,求 的值.
的值. ,当
,当 实数
实数
 为何值时,
为何值时, 为实数;
为实数; (2)
(2)