题目内容
(1)计算:
lg25+lg2-lg
-log29×log32;
(2)已知0<x<1,且x+x-1=3,求x
-x -
.
| 1 |
| 2 |
| 0.1 |
(2)已知0<x<1,且x+x-1=3,求x
| 1 |
| 2 |
| 1 |
| 2 |
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用对数的运算法则即可得出;
(2)由x+x-1=3,可得(x
-x-
)2=x+x-1-2,由于0<x<1,可得x-
>x
,即可得出.
(2)由x+x-1=3,可得(x
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)
lg25+lg2-lg
-log29×log32
=lg5+lg2-lg10-
-
×
=1+
-2=-
.
(2)∵x+x-1=3,
∴(x
-x-
)2=x+x-1-2=3-2=1,
∵0<x<1,∴x-
>x
,
∴x
-x-
=-1.
| 1 |
| 2 |
| 0.1 |
=lg5+lg2-lg10-
| 1 |
| 2 |
| 2lg3 |
| lg2 |
| lg2 |
| lg3 |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵x+x-1=3,
∴(x
| 1 |
| 2 |
| 1 |
| 2 |
∵0<x<1,∴x-
| 1 |
| 2 |
| 1 |
| 2 |
∴x
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了对数与指数的运算法则,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
下列计算:①(-2014)0=1;②2m-4=
;③x4+x3=x7;④(ab2)3=a3b6;⑤
=35,正确的是( )
| 1 |
| 2m4 |
| (-35)2 |
| A、① | B、①②③ |
| C、①③④ | D、①④⑤ |
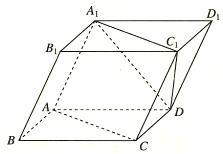 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.