题目内容
 长方体ABCD-A1B1C1D1中,E、F分别为AB、A1C的中点.
长方体ABCD-A1B1C1D1中,E、F分别为AB、A1C的中点.(1)证明:EF∥平面AA1D1D;
(2)当AA1=AD时,证明:EF⊥平面A1CD.
分析:(1)连接AD1交A1D于O,连接OF,要证明EF∥平面AA1D1D,只需证明OA∥EF即可;
(2)当AA1=AD时,要证明EF⊥平面A1CD,只需证明EF⊥A1D,EF⊥CD即可.
(2)当AA1=AD时,要证明EF⊥平面A1CD,只需证明EF⊥A1D,EF⊥CD即可.
解答: (1)证明:连接AD1交A1D于O,连接OF,显然O是AD1的中点,
(1)证明:连接AD1交A1D于O,连接OF,显然O是AD1的中点,
可得OF∥CD,OF=
CD,所以AEFO是平行四边形,所以OA∥EF,
OA?平面AA1D1D,∴EF∥平面AA1D1D
(2)当AA1=AD时,AD1⊥A1D,CD⊥AD1
由于AEFO是平行四边形,所以EF⊥A1D,CD⊥EF
A1D∩CD=D,所以EF⊥平面A1CD
 (1)证明:连接AD1交A1D于O,连接OF,显然O是AD1的中点,
(1)证明:连接AD1交A1D于O,连接OF,显然O是AD1的中点,可得OF∥CD,OF=
| 1 |
| 2 |
OA?平面AA1D1D,∴EF∥平面AA1D1D
(2)当AA1=AD时,AD1⊥A1D,CD⊥AD1
由于AEFO是平行四边形,所以EF⊥A1D,CD⊥EF
A1D∩CD=D,所以EF⊥平面A1CD
点评:本题考查直线与平面平行的判定,直线与平面垂直的判定,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
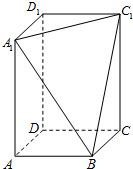 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.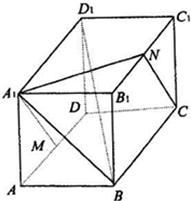 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.