题目内容
已知函数 的图象关于点(1,0)对称,且当
的图象关于点(1,0)对称,且当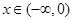 时,
时,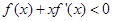 成立(其中
成立(其中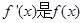 的导函数),若
的导函数),若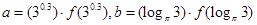 ,
,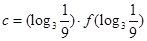 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A.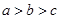 | B.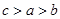 | C.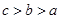 | D. |
B
解析试题分析:∵当x∈(-∞,0)时不等式f(x)+xf′(x)<0成立,即:(xf(x))′<0,∴xf(x)在 (-∞,0)上是减函数.又∵函数y=f(x-1)的图象关于点(1,0)对称,∴函数y=f(x)的图象关于点(0,0)对称,∴函数y=f(x)是定义在R上的奇函数∴xf(x)是定义在R上的偶函数∴xf(x)在 (0,+∞)上是增函数.又∵30.3>1>log23>0>log3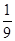 =-2,2=-log3
=-2,2=-log3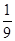 >30.3>1>log23>0,∴(-log3
>30.3>1>log23>0,∴(-log3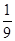 )f(-log3
)f(-log3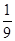 )>30.3•f(30.3)>(logπ3)•f(logπ3),即(log3
)>30.3•f(30.3)>(logπ3)•f(logπ3),即(log3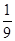 )f(log3
)f(log3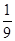 )>30.3•f(30.3)>(logπ3)•f(logπ3)即:c>a>b故选B .
)>30.3•f(30.3)>(logπ3)•f(logπ3)即:c>a>b故选B .
考点:1.函数单调性的性质;2.导数的运算;3.不等式比较大小.

练习册系列答案
相关题目
定积分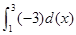 等于( )
等于( )
| A.-6 | B.6 | C.-3 | D.3 |
函数y=x2cosx的导数为( )
| A.y′=x2cosx-2xsinx | B.y′=2xcosx+x2sinx |
| C.y′=2xcosx-x2sinx | D.y′=xcosx-x2sinx |
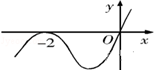
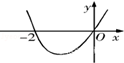
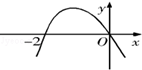
函数y=f(x)在定义域(-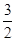 ,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )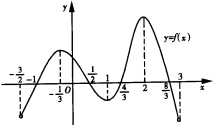
A.[- ,1]∪[2,3) ,1]∪[2,3) | B.[-1,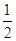 ]∪[ ]∪[ , ,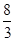 ] ] |
C.[-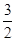 , ,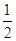 ]∪[1,2) ]∪[1,2) | D.(-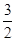 ,- ,-  ]∪[ ]∪[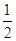 , , ]∪[ ]∪[ ,3) ,3) |
己知f(x)=xsinx,则f′(π)=( )
| A.O | B.﹣1 | C.π | D.﹣π |
若点P是曲线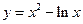 上任意一点,则点P到直线y=x-2的最小值为( ).
上任意一点,则点P到直线y=x-2的最小值为( ).
| A.1 |
B.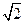 |
C.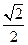 |
D.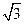 |
若函数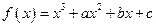 有极值点
有极值点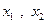 ,且
,且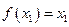 ,则关于x的方程
,则关于x的方程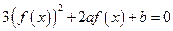 的不同实根个数是( )
的不同实根个数是( )
| A.3 | B.4 | C.5 | D.6 |
若a>0,b>0,且函数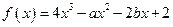 处有极值,则ab的最大值等于( ).
处有极值,则ab的最大值等于( ).
| A.2 | B.3 | C.6 | D.9 |