题目内容
(本题满分50分)设![]() ,
,![]() 为给定的整数,
为给定的整数,![]() . 对任意
. 对任意![]() 元的数集
元的数集![]() ,作
,作![]() 的所有
的所有![]() 元子集的元素和,记这些和组成的集合为
元子集的元素和,记这些和组成的集合为![]() ,集合
,集合![]() 中元素个数是
中元素个数是![]() ,求
,求![]() 的最大值.
的最大值.
![]()
解析:
![]() 的最大值为
的最大值为![]() . ……10分因
. ……10分因![]() 共有
共有![]() 个
个![]() 元子集,故显然有
元子集,故显然有![]() .…20分
.…20分
下面我们指出,对集合![]() ,相应的
,相应的![]() 等于
等于![]() ,即
,即![]() 的任意两个不同的
的任意两个不同的![]()
元子集的元素之和不相等. 从而![]() 的最大值为
的最大值为![]() .事实上,若上述的集合
.事实上,若上述的集合![]() 有两个不同的
有两个不同的![]() 元子集
元子集
![]() ,
, ![]() ,使得
,使得![]() 与
与![]() 的元素之和相等,则
的元素之和相等,则
![]() (设). ①因①可视为正整数
(设). ①因①可视为正整数![]() 的二进制表示,由于
的二进制表示,由于![]() 互不相同,
互不相同,![]() 互不相同,故由正整数的二进制表示的唯一性,我们由①推出,集合
互不相同,故由正整数的二进制表示的唯一性,我们由①推出,集合![]() 必须与
必须与![]() 相同,从而子集
相同,从而子集![]() ,矛盾.这就证明了我们的断言. 50分
,矛盾.这就证明了我们的断言. 50分

练习册系列答案
相关题目
(本题满分12分)下表是某班英语和数学成绩的分布表,已知该班有50名学生,成绩分为1~5个档次。如:表中英语成绩是4分、数学成绩是2分的人数有5人。现设该班任意一位学生的英语成绩为m,数学成绩为n。
|
n m |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英 语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
b |
6 |
0 |
a |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
(1)求m=4,n=3的概率;
(2)求在m≥3的条件下,n=3的概率;
(3)求a+b的值,并求m的数学期望;
(4)若m=2与n=4是相互独立的,求a,b的值。
 (I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量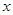 个,零件的实际出厂单价为P元,写出函数P=
个,零件的实际出厂单价为P元,写出函数P=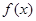 的表达式;
的表达式;