题目内容
在直角坐标系中,曲线C1的参数方程为: (
( 为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为:
为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为: ,
,
(1)求曲线C2的直角坐标方程;
(2)若P,Q分别是曲线C1和C2上的任意一点,求 的最小值.
的最小值.
(1) ;(2)
;(2)
解析
试题分析:(1)把 代入曲线C2是极坐标方程
代入曲线C2是极坐标方程 中,即可得到曲线C2的直角坐标方程;
中,即可得到曲线C2的直角坐标方程; (2)由已知可知P(
(2)由已知可知P( ),
), ,由两点间的距离公式求出
,由两点间的距离公式求出 的表达式,再根据二次函数的性质,求出
的表达式,再根据二次函数的性质,求出 的最小值,然后可得
的最小值,然后可得
 min-
min- .
.
试题解析:(1) ,
,
 . 4分
. 4分
(2)设P( ),
),
 6分
6分 时,
时, , 8分
, 8分 . 10分
. 10分
考点:1.极坐标方程和直角坐标方程的互化;2.曲线与曲线间的位置关系以及二次函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在
在 上为增函数,则称
上为增函数,则称 为“k次比增函数”,其中
为“k次比增函数”,其中 . 已知
. 已知 其中e为自然对数的底数.
其中e为自然对数的底数. 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; .
. ,
, .
. ,求证:函数
,求证:函数 是
是 上的奇函数;
上的奇函数; 上没有零点,求实数
上没有零点,求实数 的取值范围.
的取值范围. ,不等式
,不等式 的解集为
的解集为 .
. 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 表示的曲线是双曲线;命题
表示的曲线是双曲线;命题 函数
函数 在区间
在区间 上为增函数,若“
上为增函数,若“

 ”为真命题,“
”为真命题,“
 的取值范围.
的取值范围.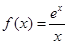 的定义域为
的定义域为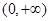 .
. 在
在 上的最小值;
上的最小值; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. =x2+
=x2+ ,求f(x);
,求f(x);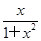 在区间[1,+∞)上是减函数.
在区间[1,+∞)上是减函数.