题目内容
(本小题满分10分)
设数列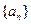 满足:
满足: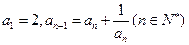 .
.
(1)证明: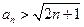 对
对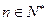 恒成立;
恒成立;
(2)令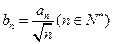 ,判断
,判断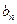 与
与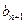 的大小,并说明理由.
的大小,并说明理由.
设数列
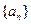 满足:
满足: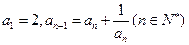 .
.(1)证明:
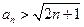 对
对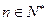 恒成立;
恒成立;(2)令
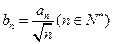 ,判断
,判断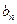 与
与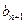 的大小,并说明理由.
的大小,并说明理由.(1)证明略
(2)
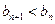
解:(1)证法一:当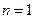 时,
时,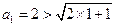 ,不等式成立,
,不等式成立,
假设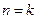 时,
时,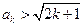 成立 (2分),
成立 (2分),
当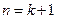 时,
时,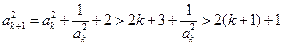 .(5分)
.(5分)
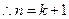 时,
时,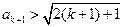 时成立
时成立
综上由数学归纳法可知,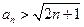 对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法二:当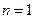 时,
时,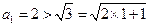 ,结论成立;
,结论成立;
假设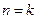 时结论成立,即
时结论成立,即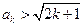 (2分)当
(2分)当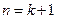 时,
时,
由函数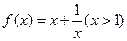 的单增性和归纳假设有
的单增性和归纳假设有
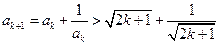 (4分),
(4分),
因此只需证: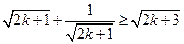 ,
,
而这等价于 ,
,
显然成立,所以当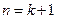 是,结论成立;
是,结论成立;
综上由数学归纳法可知,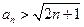 对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法三:由递推公式得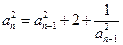 ,
,
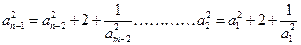 (2分)
(2分)
上述各式相加并化简得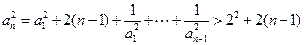
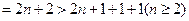 (4分)
(4分)
又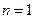 时,
时,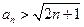 显然成立, 故
显然成立, 故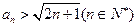 (6分)
(6分)
(2)解法一: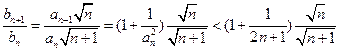 (8分)
(8分)
 (10分)
(10分)
又显然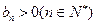 ,故
,故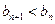 成立 (12分)
成立 (12分)
解法二: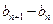
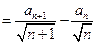
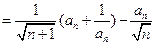
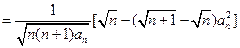
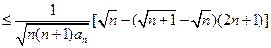 (由(1)的结论)(8分)
(由(1)的结论)(8分)
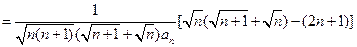 (10分)
(10分)
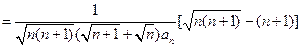
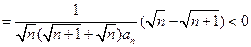
所以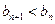 (12分)
(12分)
解法三: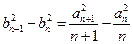
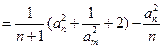 (8分)
(8分)
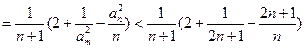 (10分)
(10分)
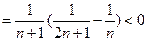
故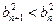 ,因此
,因此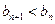 (12分)
(12分)
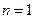 时,
时,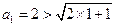 ,不等式成立,
,不等式成立,假设
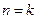 时,
时,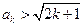 成立 (2分),
成立 (2分),当
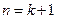 时,
时,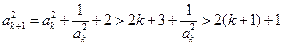 .(5分)
.(5分)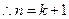 时,
时,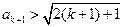 时成立
时成立综上由数学归纳法可知,
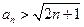 对一切正整数成立 (6分)
对一切正整数成立 (6分)证法二:当
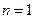 时,
时,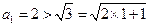 ,结论成立;
,结论成立;假设
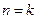 时结论成立,即
时结论成立,即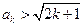 (2分)当
(2分)当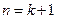 时,
时,由函数
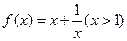 的单增性和归纳假设有
的单增性和归纳假设有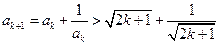 (4分),
(4分),因此只需证:
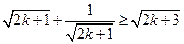 ,
,而这等价于
 ,
,显然成立,所以当
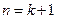 是,结论成立;
是,结论成立;综上由数学归纳法可知,
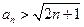 对一切正整数成立 (6分)
对一切正整数成立 (6分)证法三:由递推公式得
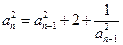 ,
,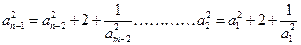 (2分)
(2分)上述各式相加并化简得
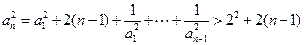
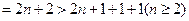 (4分)
(4分)又
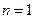 时,
时,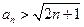 显然成立, 故
显然成立, 故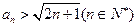 (6分)
(6分)(2)解法一:
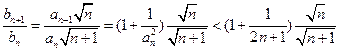 (8分)
(8分) (10分)
(10分)又显然
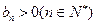 ,故
,故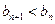 成立 (12分)
成立 (12分)解法二:
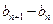
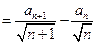
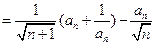
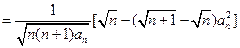
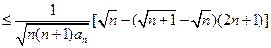 (由(1)的结论)(8分)
(由(1)的结论)(8分)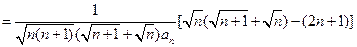 (10分)
(10分)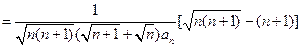
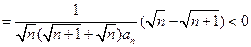
所以
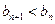 (12分)
(12分)解法三:
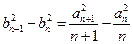
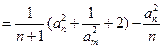 (8分)
(8分)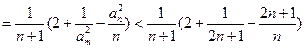 (10分)
(10分)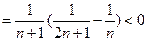
故
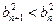 ,因此
,因此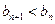 (12分)
(12分)
练习册系列答案
相关题目
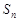 为等差数列
为等差数列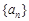 的前
的前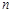 项和,且
项和,且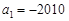 ,
,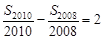 ,则
,则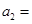 ( )
( )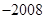
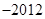
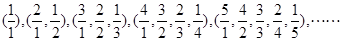
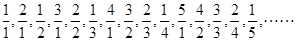
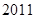 项是( )
项是( )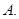
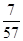
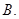
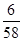
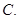
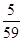
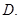
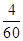
 中,
中,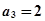 ,
, ,若
,若 为等差数列,则
为等差数列,则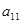 =( )。
=( )。

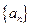 满足:
满足: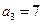 ,
,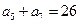 .
.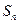 .
.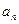 及
及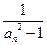 (n
(n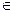 N*),求数列
N*),求数列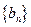 的前n项和
的前n项和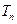
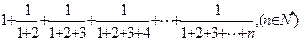 。
。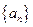 是等差数列,若
是等差数列,若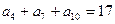 ,
,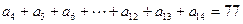 且
且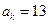 ,则
,则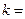 _________
_________ 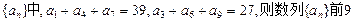 项的和
项的和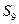 =( )
=( )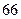 B
B 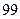 C
C 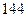 D
D