题目内容
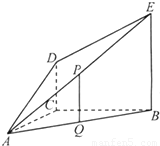
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.(I)证明:PQ∥平面ACD;
(II)证明:平面ADE⊥平面ABE;
(Ⅲ)求AD与平面ABE所成角的正弦值.
【答案】分析:(I)连接DP,CQ,利用题设条件推导出PQ DC,由此能够证明PQ∥平面ACD.
DC,由此能够证明PQ∥平面ACD.
(II)在△ABC中,由AC=BC=2,AQ=BQ,知CQ⊥AB,由DC⊥平面ABC,EB∥DC,知EB⊥平面ABC,由此能够证明平面ADE⊥平面ABE.
(Ⅲ)由(Ⅰ)知四边形DCQP是平行四边形,所以DP⊥平面ABE,由直线AD在平面ABE内的射影是AP,知直线AD与平面ABE所成角是∠DAP,由此能求出AD与平面ABE所成角的正弦值.
解答: 解:(I)证明:连接DP,CQ,在△ABE中,
解:(I)证明:连接DP,CQ,在△ABE中,
∵P,Q分别是AE,AB的中点,∴PQ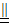
 ,
,
∵EB∥DC,AC=BC=EB=2DC=2,∴PQ DC,
DC,
∵PQ?平面ACD,DC?平面ACD,
∴PQ∥平面ACD.
(II)在△ABC中,AC=BC=2,AQ=BQ,
∴CQ⊥AB,
∵DC⊥平面ABC,EB∥DC,∴EB⊥平面ABC,
∴EB⊥CQ,∴EB⊥平面ABC.
∴EB⊥CQ,∴CQ⊥平面ABE,
∵CQ∥DP,∴DP⊥平面ABE,
∵DP?平面ADE,
∴平面ADE⊥平面ABE.
(Ⅲ)由(Ⅰ)知四边形DCQP是平行四边形,
∴DP∥CQ,
∴DP⊥平面ABE,
∴直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是∠DAP
在Rt△APD中, ,
,
DP=CQ=2sin∠CAQ=1,
∴ .
.
故AD与平面ABE所成角的正弦值为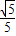 .
.
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法.解题时要认真审题,合理地化空间问题为平面问题,注意空间思维能力和推理能力的培养.
 DC,由此能够证明PQ∥平面ACD.
DC,由此能够证明PQ∥平面ACD.(II)在△ABC中,由AC=BC=2,AQ=BQ,知CQ⊥AB,由DC⊥平面ABC,EB∥DC,知EB⊥平面ABC,由此能够证明平面ADE⊥平面ABE.
(Ⅲ)由(Ⅰ)知四边形DCQP是平行四边形,所以DP⊥平面ABE,由直线AD在平面ABE内的射影是AP,知直线AD与平面ABE所成角是∠DAP,由此能求出AD与平面ABE所成角的正弦值.
解答:
 解:(I)证明:连接DP,CQ,在△ABE中,
解:(I)证明:连接DP,CQ,在△ABE中,∵P,Q分别是AE,AB的中点,∴PQ
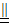
 ,
,∵EB∥DC,AC=BC=EB=2DC=2,∴PQ
 DC,
DC,∵PQ?平面ACD,DC?平面ACD,
∴PQ∥平面ACD.
(II)在△ABC中,AC=BC=2,AQ=BQ,
∴CQ⊥AB,
∵DC⊥平面ABC,EB∥DC,∴EB⊥平面ABC,
∴EB⊥CQ,∴EB⊥平面ABC.
∴EB⊥CQ,∴CQ⊥平面ABE,
∵CQ∥DP,∴DP⊥平面ABE,
∵DP?平面ADE,
∴平面ADE⊥平面ABE.
(Ⅲ)由(Ⅰ)知四边形DCQP是平行四边形,
∴DP∥CQ,
∴DP⊥平面ABE,
∴直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是∠DAP
在Rt△APD中,
 ,
,DP=CQ=2sin∠CAQ=1,
∴
 .
.故AD与平面ABE所成角的正弦值为
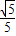 .
.点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法.解题时要认真审题,合理地化空间问题为平面问题,注意空间思维能力和推理能力的培养.

练习册系列答案
相关题目
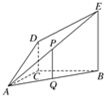 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.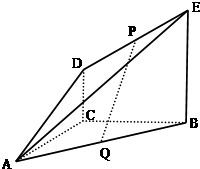 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.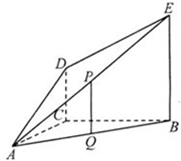 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.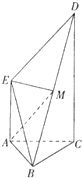 如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=
如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=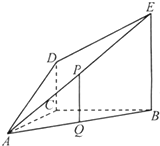 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.