Question

【题目】如图，在四棱锥S-ABCD中，底面ABCD为菱形，∠BAD=60°，平面SAD⊥平面ABCD，SA=SD，E，P，Q分别是棱AD，SC，AB的中点．

（Ⅰ）求证：PQ∥平面SAD；

（Ⅱ）求证：AC⊥平面SEQ；

（Ⅲ）如果SA=AB=2，求三棱锥S-ABC的体积．

Answer 1

【答案】1

【解析】

试题（Ⅰ）证明：取SD中点F，连结AF，PF．

因为 P，F分别是棱SC，SD的中点，

所以 FP∥CD，且FP=CD．

又因为菱形ABCD中，Q是AB的中点，

所以 AQ∥CD，且AQ =CD．

所以 FP//AQ且FP=AQ．

所以 AQPF为平行四边形．

所以 PQ//AF．

又因为平面，

平面，

所以 PQ//平面SAD ． 5分

（Ⅱ）证明：连结BD，

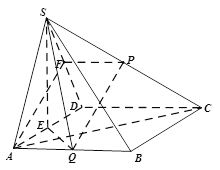
因为 △SAD中SA=SD，点E棱AD的中点，

所以 SE⊥AD．

又 平面SAD⊥平面ABCD，

平面SAD平面ABCD=AD，

SE平面，

所以 SE⊥平面ABCD，

所以SE⊥AC．

因为 底面ABCD为菱形，

E，Q分别是棱AD，AB的中点，

所以 BD⊥AC，EQ∥BD．

所以 EQ⊥AC，

因为 SEEQ=E，

所以 AC⊥平面SEQ． 11分

（Ⅲ）解：因为菱形ABCD中，∠BAD=60°，AB=2，

所以．

因为SA=AD=SD=2，E是AD的中点，所以SE=．

由（Ⅱ）可知SE⊥平面ABC，

所以三棱锥S-ABC的体积=． 14分