题目内容
设数列{an}，{bn}满足：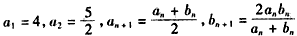
，
(Ⅰ)用an表示an+1；并证明：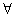
n∈N*，an＞2；
(Ⅱ)证明：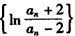
是等比数列；
(Ⅲ)设Sn是数列{an}的前n项和，当n≥2时，Sn与2（n+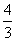
）是否有确定的大小关系？若有，加以证明；若没有，请说明理由。
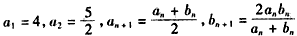，(Ⅰ)用an表示an+1；并证明：
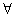n∈N*，an＞2； (Ⅱ)证明：
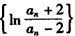是等比数列；(Ⅲ)设Sn是数列{an}的前n项和，当n≥2时，Sn与2（n+
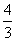）是否有确定的大小关系？若有，加以证明；若没有，请说明理由。 解：(Ⅰ)由已知，得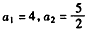
，
所以，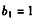
，
故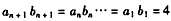
，
由已知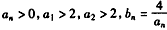
，
∴
，
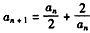由基本不等式，得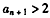
，
故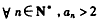
。
(Ⅱ)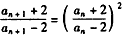
，
，
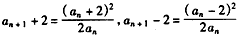所以，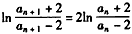
，
所以，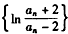
是等比数列。
(Ⅲ)由(Ⅱ)可知，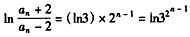
，
∴
，
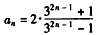当n≥2时，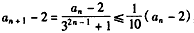
，
∴
，
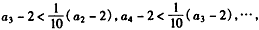
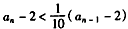相加，得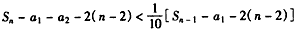
，
∵
，
∴
，
∴
，
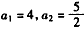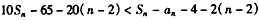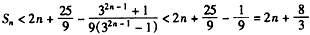故n≥2时，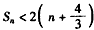
。
解法二：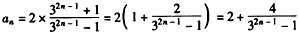
，
设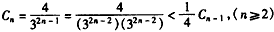
，
，
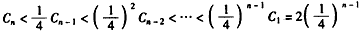∴当n≥2时，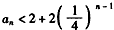
，
。
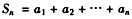
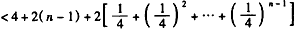
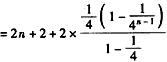
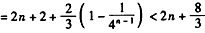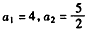，所以，
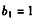，故
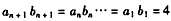，由已知
，∴
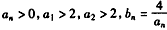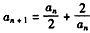，由基本不等式，得
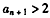，故
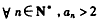。(Ⅱ)
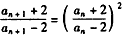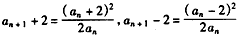，，所以，
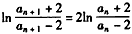，所以，
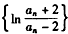是等比数列。(Ⅲ)由(Ⅱ)可知，
，∴
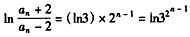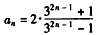，当n≥2时，
，∴
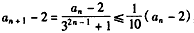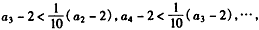
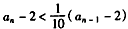，相加，得
，∵
，∴
，∴
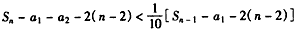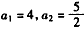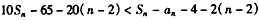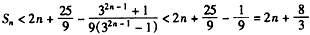，故n≥2时，
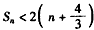。解法二：
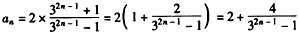，设
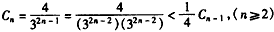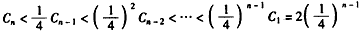，，∴当n≥2时，
，。
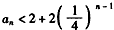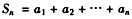
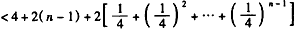
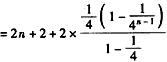
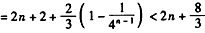练习册系列答案
相关题目