题目内容
设xi∈R(i=1,2,…,n),n≥3,p=(2)|xi-![]() |≤
|≤![]() .
.
证明:(1)因为![]() =p2-2p,根据柯西不等式得
=p2-2p,根据柯西不等式得
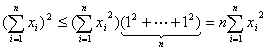 ,
,
∴p2≤n(p2-2q)![]() p2-2q≥0.
p2-2q≥0.
(2)由已知得x1+…+xi-1+xi+1+…+xn=p-xi,且x12+…+xi-12+xi+12+…+xn2=p2-2q-xi2
∴(p-xi)2≤(p2-2q-xi2)(n-1).
化简整理得
(xi-![]() )2≤(
)2≤(![]() )2p2-
)2p2-![]() q
q![]() |xi-
|xi-![]() |≤
|≤![]() .
.

练习册系列答案
相关题目
题目内容
设xi∈R(i=1,2,…,n),n≥3,p=(2)|xi-![]() |≤
|≤![]() .
.
证明:(1)因为![]() =p2-2p,根据柯西不等式得
=p2-2p,根据柯西不等式得
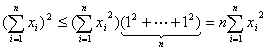 ,
,
∴p2≤n(p2-2q)![]() p2-2q≥0.
p2-2q≥0.
(2)由已知得x1+…+xi-1+xi+1+…+xn=p-xi,且x12+…+xi-12+xi+12+…+xn2=p2-2q-xi2
∴(p-xi)2≤(p2-2q-xi2)(n-1).
化简整理得
(xi-![]() )2≤(
)2≤(![]() )2p2-
)2p2-![]() q
q![]() |xi-
|xi-![]() |≤
|≤![]() .
.
