题目内容
(本小题满分12分)
已知函数 (其中
(其中 ,
, ,
, )的最大值为2,最小正周
)的最大值为2,最小正周
期为 .
.
(1)求函数 的解析式;
的解析式;
(2)若函数 图象上的两点
图象上的两点 的横坐标依次为
的横坐标依次为 ,
, 为坐标原点,求△
为坐标原点,求△ 的
的
面积.
【答案】
(1) (2)
(2)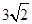
【解析】
试题分析:(1)解:∵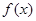 的最大值为2,且
的最大值为2,且 , ∴
, ∴ .
.
∵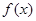 的最小正周期为
的最小正周期为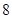 , ∴
, ∴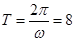 ,得
,得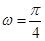 .
.
∴ .
.
(2)解法1:∵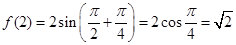 ,
,
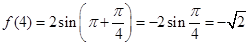 ,
,
∴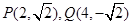 .
.
∴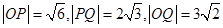 .
.
∴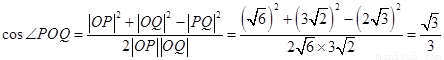 .
.
∴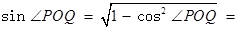
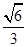 .
.
∴△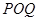 的面积为
的面积为
 .
.
解法2:∵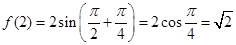 ,
,
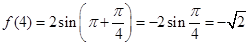 ,
,
∴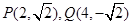 .∴
.∴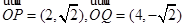 .
.
∴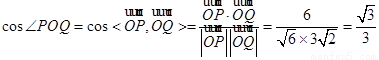 .
.
∴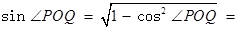
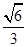 .
.
∴△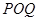 的面积为
的面积为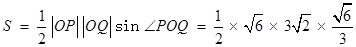
 .
.
解法3:∵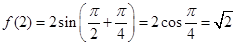 ,
,
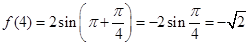 ,
,
∴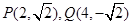 .
.
∴直线 的方程为
的方程为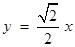 ,即
,即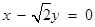 .
.
∴点 到直线
到直线 的距离为
的距离为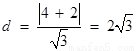 .
.
∵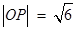 ,
,
∴△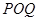 的面积为
的面积为
 .
.
考点:求三角函数解析式及解三角形
点评:解析式中A值与最值有关,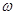 值与周期有关
值与周期有关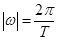 ;第二问解三角形一般用正余弦定理寻找边角间的关系,正弦定理:
;第二问解三角形一般用正余弦定理寻找边角间的关系,正弦定理: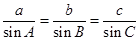 ,余弦定理
,余弦定理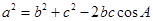 ,
,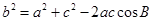 ,
,

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目