题目内容
2.在△ABC内随机取一点P,使$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x≤$\frac{2}{3}$在的条件下y≥$\frac{1}{3}$的概率( )| A. | $\frac{7}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 根据题意,把问题转化为求二元一次不等式组表示的平面区域问题,根据区域面积的比值求概率的应用问题,即可求出对应的概率.
解答 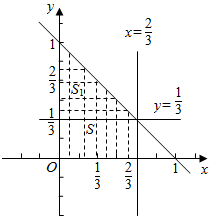 解:△ABC内随机取一点P,使$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,
解:△ABC内随机取一点P,使$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,
则0≤x+y≤1;
又x≤$\frac{2}{3}$,
则由$\left\{\begin{array}{l}{0≤x+y≤1}\\{0≤x≤\frac{2}{3}}\end{array}\right.$所围成的区域面积为
S=$\frac{1}{2}$×12-$\frac{1}{2}$×${(\frac{1}{3})}^{2}$=$\frac{4}{9}$;
由$\left\{\begin{array}{l}{0≤x+y≤1}\\{0≤x≤\frac{2}{3}}\\{y≥\frac{1}{3}}\end{array}\right.$所围成的区域面积为
S1=$\frac{1}{2}$×${(\frac{2}{3})}^{2}$=$\frac{2}{9}$,
所以,所求的概率为
P=$\frac{{S}_{1}}{S}$=$\frac{\frac{2}{9}}{\frac{4}{9}}$=$\frac{1}{2}$.
故选:C.
点评 本题主要考查几何槪型的概率计算问题,解题的关键是把问题转化为求二元一次不等式组表示的平面区域面积,是综合性题目.

练习册系列答案
相关题目
17.已知函数$f(x)=\left\{\begin{array}{l}m\sqrt{1-{x^2}},x∈({-1,1}]\\ 1-|{x-2}|,x∈({1,3}]\end{array}\right.$,其中m>0,且函数f(x)=f(x+4),若方程3f(x)-x=0恰有5个根,则实数m的取值范围是( )
| A. | $(\frac{{\sqrt{15}}}{3},\sqrt{7})$ | B. | $(\frac{{\sqrt{15}}}{3},\frac{8}{3})$ | C. | $(\frac{4}{3},\sqrt{7})$ | D. | $(\frac{4}{3},\frac{8}{3})$ |
11.已知函数$f(x)=\sqrt{3}sinωx+cosωx$(ω>0)的最小正周期为4π,则该函数的图象( )
| A. | 关于直线x=$\frac{π}{3}$对称 | B. | 关于直线x=$\frac{5π}{3}$对称 | ||
| C. | 关于点($\frac{π}{3}$,0)对称 | D. | 关于点($\frac{5π}{3}$,0)对称 |
12.已知(1+x)(1-ax)6展开式中x2项的系数为21,则实数a=( )
| A. | ±$\frac{\sqrt{35}}{5}$ | B. | $-\frac{7}{2}$ | C. | 1或$-\frac{7}{5}$ | D. | -1或$\frac{7}{5}$ |