题目内容
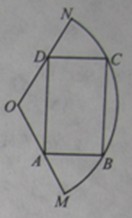
如图,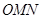 是半径为2,圆心角为
是半径为2,圆心角为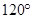 的扇形,
的扇形,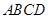 是扇形的内接矩形.
是扇形的内接矩形.
(Ⅰ)当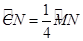 时,求
时,求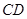 的长;
的长;
(Ⅱ)求矩形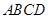 面积的最大值.
面积的最大值.
 是半径为2,圆心角为
是半径为2,圆心角为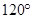 的扇形,
的扇形, 是扇形的内接矩形.
是扇形的内接矩形.(Ⅰ)当
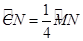 时,求
时,求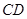 的长;
的长;(Ⅱ)求矩形
 面积的最大值.
面积的最大值.
(Ⅰ)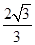 (Ⅱ)
(Ⅱ)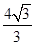
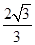 (Ⅱ)
(Ⅱ)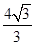
试题分析:(Ⅰ)由图形的对称性作出辅助线,用三角函数求出相关线段长度;(Ⅱ)设∠EOC=θ,与(Ⅰ)类似用三角函数表示出相关线段长度和矩形ABCD的面积,继而求关于θ的三角函数的最大值.
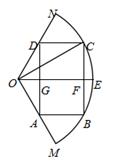
试题解析:如图,记
 的中点为E,连结OE,OC,交BC于F,交AD于G,则∠DOG=60°.
的中点为E,连结OE,OC,交BC于F,交AD于G,则∠DOG=60°.设∠EOC=θ(0°<θ<60°).
(Ⅰ)当
 =
=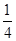
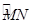 时,θ=30°.
时,θ=30°.在Rt△COF中,OF=OCcos30°=
 ,CF=OCsin30°=1.
,CF=OCsin30°=1.在Rt△DOG中,DG=CF=1,OG=
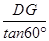 =
=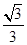 .
.所以CD=GF=OF-OG=
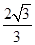 .
.(Ⅱ)与(Ⅰ)同理,
BC=2CF=4sinθ,CD=OF-OG=2cosθ-
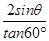 =2cosθ-
=2cosθ-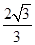 sinθ.
sinθ.则矩形ABCD的面积
S=BC·CD=4sinθ(2cosθ-
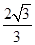 sinθ)=4sin2θ-
sinθ)=4sin2θ-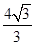 (1-cos2θ)=
(1-cos2θ)=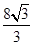 sin(2θ+30°)-
sin(2θ+30°)-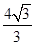 .
.因为30°<2θ+30°<150°,故当2θ+30°=90°,
即θ=30°时,S取最大值
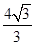 .
.
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
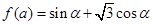 ,其中,角
,其中,角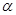 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与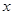 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点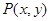 ,且
,且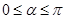 .
.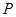 点的坐标为(-
点的坐标为(-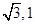 ),求
),求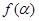 的值;
的值;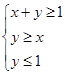 上的一个动点,试确定角
上的一个动点,试确定角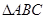 中,角
中,角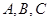 所对的边分别为
所对的边分别为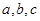 且满足
且满足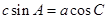 .
. 的大小;
的大小;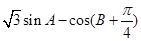 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的大小.
的大小.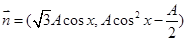 ,
,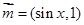 ,
,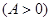 ,函数
,函数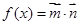 的最大值为
的最大值为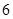 .
.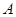 ;
;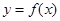 的图像向左平移
的图像向左平移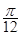 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的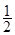 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数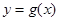 的图像,求
的图像,求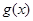 在
在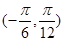 上的值域.
上的值域.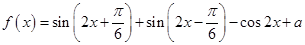 (
(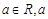 为常数).
为常数).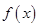 的最小正周期和单调增区间;
的最小正周期和单调增区间;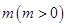 个单位后,得到函数
个单位后,得到函数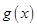 的图像关于
的图像关于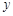 轴对称,求实数
轴对称,求实数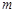 的最小值.
的最小值. , 分别设
, 分别设 的面积为
的面积为 .
.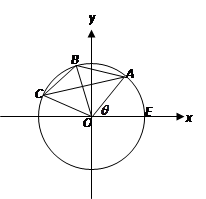
 表示
表示 的最大值及取最大值时
的最大值及取最大值时 的值.
的值. ,计算:
,计算: ;(2)
;(2)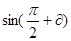 ;(3)
;(3) ;(4)
;(4) ;
; ,则AB= .
,则AB= .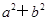 =2014
=2014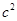 ,则
,则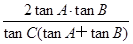 的值为( )
的值为( )