题目内容
20.过点A(0,-1)作直线l交抛物线y2=4x于B,C两点,求BC中点P的轨迹方程.分析 设点作差,即可求BC中点P的轨迹方程.
解答 解:设P(x,y),B(x1,y1),C(x2,y2),则直线的斜率为$\frac{y+1}{x}$
∵y12=4x1,y22=4x2,
∴作差整理可得$\frac{y+1}{x}$=$\frac{4}{2y}$,
∴y2+y-2x=0,
∴BC中点P的轨迹方程是y2+y-2x=0.
点评 本题考查轨迹方程,考查点差法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
5.设奇函数f(x)满足f(x)=$\left\{\begin{array}{l}{-1(x≥1)}\\{1(0<x<1)}\end{array}\right.$,则f[f(sin6)]=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.与平面向量$\overrightarrow{a}$=(-$\frac{1}{3}$,-$\frac{2}{3}$)垂直的单位向量的坐标为( )
| A. | ($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) | B. | (-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$) | ||
| C. | ($\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$)或(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$) | D. | ($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$)或(-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$) |
10.已知x,y满足约束条件$\left\{\begin{array}{l}{2y-x-1≥0}\\{2y-3x+1≤0}\\{2y+x-11≤0}\end{array}\right.$,z=ax+by(a>b>0)最大值为12,则$\frac{5}{a}$+$\frac{2}{b}$的最小值为( )
| A. | $\frac{31+10\sqrt{6}}{12}$ | B. | $\frac{23+4\sqrt{30}}{12}$ | C. | $\frac{7+2\sqrt{10}}{12}$ | D. | 4 |
 如图,正方体ABCD-A1B1C1D1中,E,F分别是B1C1,C1D1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别是B1C1,C1D1的中点.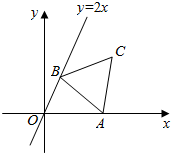 如图,在x轴上有动点A,直线y=2x上有动点B,定点C(4,3),当△ABC的周长最小时,求A,B两点的坐标.
如图,在x轴上有动点A,直线y=2x上有动点B,定点C(4,3),当△ABC的周长最小时,求A,B两点的坐标.