题目内容

若实数a、b、c、d满足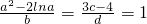 $数学公式$ ，则（a-c）²+（b-d）²的最小值为________．

$\text{[math]}$
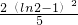
分析：由 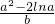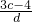$\text{[math]}$ = $\text{[math]}$ =1可知点P（a，b）是曲线y=x²-2lnx上的点，Q（c，d）是直线y=3x-4上的点，由导数的几何意义可知，过曲线y=x²-2lnx上的点P（a，b）且与线y=3x-4平行时，|PQ|²=（a-c）²+（b-d）²有最小值．
解答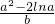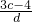：∵ $\text{[math]}$ = $\text{[math]}$ =1，
∴点P（a，b）是曲线f（x）=x²-2lnx（x＞0）上的点，Q（c，d）是直线y=3x-4上的点，
∴|PQ|²=（a-c）²+（b-d）²．
要使|PQ|²最小，当且仅当过曲线y=x²-2lnx上的点P（a，b）且与线y=3x-4平行时．
∵f′（x）=2x- 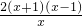$\text{[math]}$ = $\text{[math]}$ （x＞0），
由f′（x）＞0得，x＞1；由f′（x）＜0得0＜x＜1．
∴当x=1时，f（x）取得极小值，为1．
作图如下：

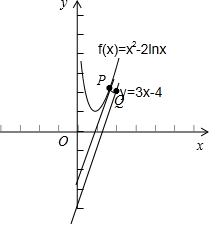
∵f′（x）|_x=a=2a- $\text{[math]}$ ，直线y=3x-4的斜率k=3，
∴2a- $\text{[math]}$ =3，
∴a=2或a=- $\text{[math]}$ （由于a＞0，故舍去）．
∴b=2²-2ln2=4-2ln2．
设点P（2，4-2ln2）到直线y=3x-4的距离为d，则d²= $\text{[math]}$ = $\text{[math]}$ ．
∵|PQ|²≥d²= $\text{[math]}$ ，
∴（a-c）²+（b-d）²的最小值为 $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题考查函数最值的应用，分析得到点P（a，b）是曲线y=x²-2lnx上的点，Q（c，d）是直线y=3x-4上的点，|PQ|²=（a-c）²+（b-d）²是关键，也是难点，考查理解题意与等价转化思想的综合应用，考查导数的几何意义及点到直线间的距离，属于难题．