Question

设函数f(x)=-ax,其中a＞0,解不等式f(x)≤1.

Answer 1

思路分析:本题首先由根式定义域x²+1≥1出发,其次,由x的系数(a²-1)确定系数a分为a≥1,0＜a＜1两个区间讨论.研究函数的单调性,总是从表述f(x₁)-f(x₂)入手,研究其大小关系,本题则是在a≥1的情况下,判定

f(x₁)-f(x₂)的正负.

解法一:不等式f(x)≤1,即≤1+ax,

由此可得1≤1+ax,又由a＞0知x≥0,所以原不等式等价于

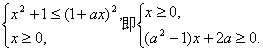
所以,当a≥1时,解为x≥0.

当0＜a＜1时,解为0≤x≤.

解法二:f(x)≤1等价于不等式组

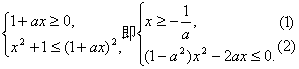
当a＞1时,由（2）得x≤或x≥0.

因为-(-)=＜0,

所以,由（1）（2）可得x≥0.

当a=1时,由（2）可得x≥0.

当0＜a＜1时,由（2）可得0≤x≤.

总之,a≥1时,x≥;0＜a＜1时,0≤x≤.

解法三:由f(x)≤1,即得≤1+ax.

∵1≤,∴1≤1+ax.

由a＞0得x≥0.

令tanθ=x,θ∈［0,］,

则≤1+ax化为secθ≤1+atanθ,

∴1≤cosθ+asinθ,

即1≤1-2sin²+2asincos.

也就是sin²≤a·sincos.

①若sin=0,则上式恒成立.此时,=0,即x=0.

②若sin＞0,则cos＞0,则上式化为a≥tan.

∵∈(0,),∴tan∈(0,1).∴当a≥1时,a≥tan恒成立.此时x=tanθ＞0.

当0＜a＜1时,0＜x=tanθ=.

总之,当a≥1时,原不等式的解集为［0,+∞］;当0＜a＜1时,原不等式的解集为［0,］.