题目内容
平面内与两定点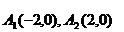 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数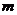 的点的轨迹,加上
的点的轨迹,加上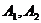 两点,所成的曲线
两点,所成的曲线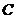 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(I)求曲线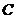 的方程,并讨论
的方程,并讨论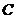 的形状与
的形状与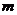 值的关系.
值的关系.
(Ⅱ)当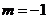 时,对应的曲线为
时,对应的曲线为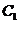 ;对给定的
;对给定的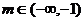 ,对应的曲线为
,对应的曲线为 ,若曲线
,若曲线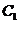 的斜率为
的斜率为 的切线与曲线
的切线与曲线 相交于
相交于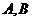 两点,且
两点,且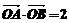 (
(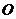 为坐标原点),求曲线
为坐标原点),求曲线 的方程.
的方程.
【答案】
解:(I)设动点为M,其坐标为 ,
,
当 时,由条件可得
时,由条件可得 ,
,
即 ,
,
又 的坐标满足
的坐标满足 ,
,
故依题意,曲线 的方程为
的方程为 .--------------3分
.--------------3分
当 曲线
曲线 的方程为
的方程为 ,
, 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是圆心在原点,半径为2的圆;
是圆心在原点,半径为2的圆;
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线 的方程为
的方程为 ,
, 是焦点在
是焦点在 轴上的双曲线.
轴上的双曲线.
--------6分
(Ⅱ)曲线 ;
; ,
, :
: ,
,
设圆 的斜率为
的斜率为 的切线
的切线 和椭圆
和椭圆 交于A(x1,y1),B(x2,y2)两点,
交于A(x1,y1),B(x2,y2)两点,
令直线AB的方程为 ,①
,①
将其代入椭圆 的方程并整理得
的方程并整理得

由韦达定理得
 ②
②
因为  ,
,
所以  ③
③
将①代入③并整理得

联立②得
 ④
④
因为直线AB和圆 相切,
相切,
因此 ,
, ,
,
由④得
所以曲线 的方程
的方程 ,即
,即 .-------12分
.-------12分

练习册系列答案
相关题目
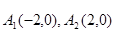 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数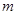 的点的轨迹,加上
的点的轨迹,加上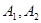 两点,所成的曲线
两点,所成的曲线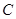 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.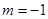 时,对应的曲线为
时,对应的曲线为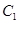 ;对给定的
;对给定的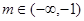 ,对应的曲线为
,对应的曲线为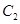 ,若曲线
,若曲线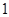 的切线与曲线
的切线与曲线 两点,且
两点,且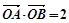 (
(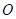 为坐标原点),求曲线
为坐标原点),求曲线 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数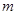 的点的轨迹,加上
的点的轨迹,加上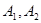 两点,所成的曲线
两点,所成的曲线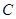 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.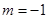 时,对应的曲线为
时,对应的曲线为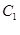 ;对给定的
;对给定的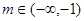 ,对应的曲线为
,对应的曲线为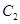 ,若曲线
,若曲线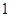 的切线与曲线
的切线与曲线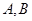 两点,且
两点,且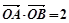 (
(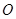 为坐标原点),求曲线
为坐标原点),求曲线