题目内容
设点A(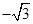 ,0),B(
,0),B(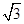 ,0),直线AM、BM相交于点M,且它们的斜率之积为
,0),直线AM、BM相交于点M,且它们的斜率之积为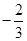 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)若直线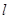 过点F(1,0)且绕F旋转,
过点F(1,0)且绕F旋转,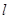 与圆
与圆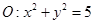 相交于P、Q两点,
相交于P、Q两点,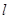 与轨迹C相交于R、S两点,若|PQ|
与轨迹C相交于R、S两点,若|PQ|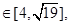 求△
求△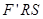 的面积的最大值和最小值(F′为轨迹C的左焦点).
的面积的最大值和最小值(F′为轨迹C的左焦点).
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ,
,
解析试题分析:(Ⅰ)根据椭圆的定义、几何性质可求;(Ⅱ)直线与椭圆相交,联立消元,设点代入化简,利用基本不等式求最值.
试题解析:(Ⅰ)设 ,则
,则
化简
 轨迹
轨迹 的方程为
的方程为
(Ⅱ)设 ,
, 的距离
的距离 ,
,
 ,将
,将 代入轨迹
代入轨迹 方程并整理得:
方程并整理得:
设 ,则
,则 ,
,


设 ,则
,则 上递增,
上递增,

 ,
,
考点:椭圆,根与系数关系,基本不等式,坐标表示

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
 的直线过抛物线
的直线过抛物线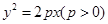 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.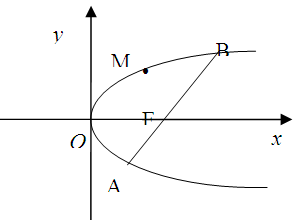
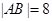 ,求抛物线的方程;
,求抛物线的方程;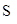 的最大值.
的最大值.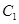 的参数方程为
的参数方程为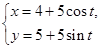 (
(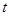 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线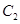 的极坐标方程为
的极坐标方程为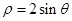 .
.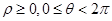 ).
).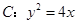 焦点为
焦点为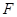 ,直线
,直线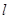 经过点
经过点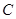 相交于
相交于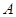 ,
, 两点
两点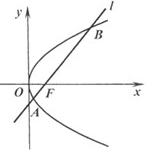
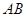 的中点在直线
的中点在直线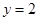 上,求直线
上,求直线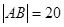 ,求直线
,求直线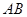 长为2m,跳水板距水面
长为2m,跳水板距水面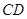 的高
的高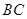 为3m,
为3m, =5m,
=5m,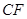 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点 m(
m(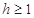 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以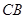 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.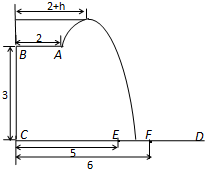
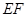 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时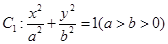 的离心率为
的离心率为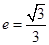 ,直线
,直线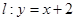 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆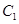 的短半轴长为半径的圆
的短半轴长为半径的圆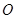 相切.
相切.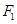 ,右焦点为
,右焦点为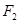 ,直线
,直线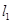 过点
过点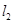 垂直于
垂直于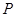 ,线段
,线段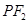 的垂直平分线交
的垂直平分线交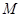 ,求点
,求点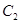 的方程;
的方程; 轴交于点
轴交于点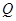 ,不同的两点
,不同的两点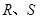 在
在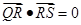 ,求
,求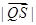 的取值范围.
的取值范围.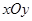 中,已知点
中,已知点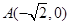 ,
,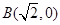 ,
,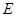 为动点,且直线
为动点,且直线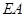 与直线
与直线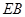 的斜率之积为
的斜率之积为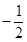 .
.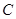 的方程;
的方程;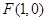 的直线
的直线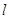 与曲线
与曲线 ,
, .若点
.若点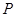 在
在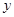 轴上,且
轴上,且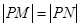 ,求点
,求点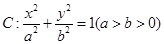 的离心率为
的离心率为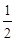 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线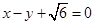 相切,直线
相切,直线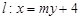 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.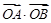 的取值范围;
的取值范围; 的对称中心为坐标原点,上焦点为
的对称中心为坐标原点,上焦点为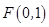 ,离心率
,离心率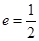 .
.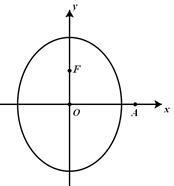
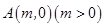 为
为 轴上的动点,过点
轴上的动点,过点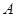 作直线
作直线 与直线
与直线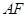 垂直,试探究直线
垂直,试探究直线