棱长为2的正方体ABCD-A1B1C1D1中.M是棱AA1的中点.过C.M.D1作正方体的截面.则截面的面积是．题目和参考答案——青夏教育精英家教网——

题目内容

棱长为2的正方体ABCD-A₁B₁C₁D₁中，M是棱AA₁的中点，过C、M、D₁作正方体的截面，则截面的面积是

．

分析：由点、线、面的位置关系作出截面，依据图形求出面积即可．

解答：

解：如图，由面面平行的性质知截面与平面AB₁的交线MN是△AA₁B的中位线，所以截面是梯形CD₁MN，
易求其面积为

9

2

．

点评：考查空间中截面的作法及梯形的面积公式．

练习册系列答案

课程导学系列答案

Top巅峰特训系列答案

新课堂新坐标高三一轮总复习系列答案

百年学典全优课堂高考总复习系列答案

新课标高考总复习创新方案系列答案

金版学案高考总复习系列答案

三维设计新课标高考总复习系列答案

单元滚动检测卷系列答案

每周6加13读3练1周1测系列答案

一品课堂通关测评系列答案

相关题目

在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E，F分别为棱AB和CC₁的中点，则线段EF被正方体的内切球球面截在球内的线段长为

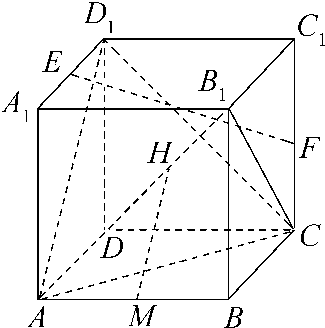如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F、M、H分别为A₁D₁、CC₁、AB、DB₁的中点．
（1）求证：EF∥平面ACD₁；
（2）求证：MH⊥B₁C；
（3）在棱BB₁上是否存在一点P，使得二面角P-AC-B的大小为30°？若存在，求出BP的长；若不存在，请说明理由．

在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F分别为A₁D₁和CC₁的中点
（1）求证：EF∥平面A₁C₁B；
（2）求异面直线EF与AB所成角的余弦值．

在棱长为2的正方体ABCD-A₁B₁C₁D₁中，点E，F分别是棱AB，BC的中点，则点C₁到平面B₁EF的距离是（　　）

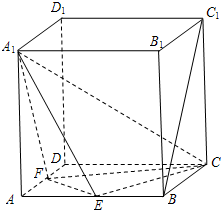（2007•静安区一模）（文）如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，点E、F分别是棱AB、AD的中点．求：
（1）异面直线BC₁与EF所成角的大小；
（2）三棱锥A₁-EFC的体积V．