题目内容
设在同一个平面上的两个非零的不共线向量
,
满足
⊥(
-
),若|
|=2,|
|=1,则|
-
x|(x∈R)取值范围是 .
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
分析:由两个非零的不共线向量
,
满足
⊥(
-
),知
•
-
2=0,由|
|=2,|
|=1,知
•
=1,故|
-
x|2=
2+x2
2-2x
•
=4+x2-2x=(x-1)2+3≥3,由此能求出|
-
x|(x∈R)取值范围.
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:解:∵两个非零的不共线向量
,
满足
⊥(
-
),
∴
•(
-
)=0,即
•
-
2=0,
∵|
|=2,|
|=1,
∴
•
=1,
|
-
x|2=
2+x2
2-2x
•
=4+x2-2x=(x-1)2+3≥3
∴|
-
x|(x∈R)取值范围是[
,+∞).
故答案为:[
,+∞).
| a |
| b |
| b |
| a |
| b |
∴
| b |
| a |
| b |
| a |
| b |
| b |
∵|
| a |
| b |
∴
| a |
| b |
|
| a |
| b |
| a |
| b |
| a |
| b |
∴|
| a |
| b |
| 3 |
故答案为:[
| 3 |
点评:本题考查数量积判断两个平面向量的垂直关系的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 满足
满足 ,若
,若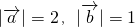 ,则
,则 取值范围是________.
取值范围是________.