题目内容

数列{an}满足a1=1,an=an-1+1(n≥2),

(1)若bn=an-2，求证：{bn}为等比数列；

(2)求{an}的通项公式及前n项和公式Sn.

(1)证明：由an=an-1+1,得

an-2=(an-1-2),

即=(n≥2).

∴{bn}是以-1为首项，公比为的等比数列.

(2)解：bn=(-1)()n-1,即an-2=-()n-1.

∴an=2-()n-1.

故Sn=a1+a2+…+an

=2n-(1+++…+)

=2n-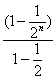=2n-2+.

练习册系列答案
相关题目
设b＞0，数列{an}满足a1=b，an=
nban-1an-1+n-1
（n≥2）
（1）求数列{an}的通项公式；
（4）证明：对于一切正整数n，2an≤bn+1+1．
若数列{an}满足a1=1，a2=2，an=
an-1an-2
(n≥3)，则a17等于
 
．
已知a＞0，数列{an}满足a1=a，an+1=a+
1
an
，n=1，2，….
（I）已知数列{an}极限存在且大于零，求A=
lim
n→∞
an（将A用a表示）；
（II）设bn=an-A，n=1，2，…，证明：bn+1=-
bn
A(bn+A)
；
（III）若|bn|≤
1
2n
对n=1，2，…都成立，求a的取值范围．
数列{an}满足a1=1，an=
12
an-1+1(n≥2)
（1）若bn=an-2，求证{bn}为等比数列；    
（2）求{an}的通项公式．
数列{an}满足a1=
4
3
，an+1=an2-an+1（n∈N*），则m=
1
a1
+
1
a2
+…+
1
a2013
的整数部分是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网