题目内容
已知集合A={x丨x2-ax+a2-19=0}，B={x丨x2-5x+6=0}，C={x丨x2+2x-8=0}，若∅?（A∩B）与A∩C=∅同时成立，求实数a的值．
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：求出集合B，C，由∅?（A∩B）与A∩C=∅同时成立确定-4∉A，2∉A，3∈A．代入x2-ax+a2-19=0求a并验证．
解答：
解：B={x丨x2-5x+6=0}={2，3}，C={x丨x2+2x-8=0}={-4，2}，
由∅?（A∩B）与A∩C=∅同时成立知，
-4∉A，2∉A，3∈A．
则9-3a+a2-19=0
即a2-3a-10=0
解得，a=5，或a=-2．
若a=5，则A=B，不成立．
若a=-2，则x=-5或x=3，成立．
综上所述，a=-2．
由∅?（A∩B）与A∩C=∅同时成立知，
-4∉A，2∉A，3∈A．
则9-3a+a2-19=0
即a2-3a-10=0
解得，a=5，或a=-2．
若a=5，则A=B，不成立．
若a=-2，则x=-5或x=3，成立．
综上所述，a=-2．
点评：本题考查了集合间的运算，及相互关系，注意验证．
练习册系列答案
阅读快车系列答案
相关题目
下列各数中最小的数是（ ）
| A、85（9） |
| B、100 |
| C、111111（2） |
| D、210（6） |
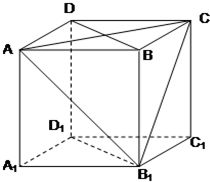在正方体ABCD-A1B1C1D1中，