题目内容
【题目】已知圆
经过点
、
，并且直线
： 
平分圆
.
（Ⅰ）求圆
的方程；
（Ⅱ）若过点
，且斜率为
的直线
与圆
有两个不同的交点
.
（ⅰ）求实数
的取值范围；
（ⅱ）若
，求
的值.
【答案】（Ⅰ）
；（Ⅱ）（ⅰ）
，（ⅱ）
.
【解析】试题分析：（Ⅰ）确定圆需要三个条件，求圆方程可用待定系数法或直接法，此处是充分运用平几知识，求出圆心和半径，直接写方程；（Ⅱ）直线与圆的关系既可用几何法，也可运用代数法，这里两种方法都用了，感受一下，何时用何法的内在规律，韦达定理一定要和判别式结合使用，否则易犯错.
试题解析：（Ⅰ）线段
的中点
， 
，故线段
的中垂线方程为
，即
.
因为圆
经过
两点，故圆心在线段
的中垂线上.
又因为直线
： 
平分圆
，所以直线
经过圆心.
由
解得
，即圆心的坐标为
，而圆的半径
，所以圆
的方程为： 
5分
（Ⅱ）直线
的方程为
.
圆心
到直线
的距离
，
（ⅰ）由题意得
，两边平方整理得： 
解之得
8分
（ⅱ）将直线
的方程与圆
的方程组成方程组得： 
消去
，整理得
10分
设
，则由根与系数的关系可得：
， 
而
所以
12分
故有
，解得
.经检验知，此时有
，所以
14分
备战中考寒假系列答案
【题目】简阳羊肉汤已入选成都市级非遗项目，成为简阳的名片。当初向各地作了广告推广，同时广告对销售收益也有影响。在若干地区各投入4万元广告费用，并将各地的销售收益绘制成频率分布直方图（如图所示）．由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的．
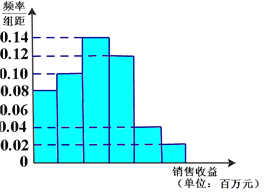
（Ⅰ）根据频率分布直方图，计算图中各小长方形的宽度；
（Ⅱ）根据频率分布直方图，估计投入4万元广告费用之后，并将各地销售收益的平均值（以各组的区间中点值代表该组的取值）；
（Ⅲ）按照类似的研究方法，测得另外一些数据，并整理得到下表：
广告投入x（单位：万元） | 1 | 2 | 3 | 4 | 5 |
销售收益y（单位：百万元） | 2 | 3 | 2 | 7 |
表中的数据显示，
与
之间存在线性相关关系，请将（Ⅱ）的结果填入空白栏，并计算关于的回归方程．回归直线的斜率和截距的最小二乘估计公式分别为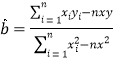
,
．
