题目内容
17.函数f(x)对任意的a,b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x>0时f(x)>1,(1)求证:f(x)在R上是增函数;
(2)若f(2)=3,解不等式f(3m2-m-2)<3.
分析 (1)先任取x1<x2,x2-x1>0.由当x>0时,f(x)>1.得到f(x2-x1)>1,再对f(x2)按照f(a+b)=f(a)+f(b)-1变形得到结论.
(2)由f(2)=3,再将f(3m2-m-2)<3转化为f(3m2-m-2)<f(2),由(1)中的结论,利用单调性求解.
解答 解:(1)证明:任取x1<x2,
∴x2-x1>0.
∴f(x2-x1)>1.
∴f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1)-1>f(x1),
∴f(x)是R上的增函数.
(2)∵f(2)=3.
∴f(3m2-m-2)<3=f(2).
又由(1)的结论知,f(x)是R上的增函数,
∴3m2-m-2<2,
3m2-m-4<0,
∴-1<m<$\frac{4}{3}$即不等式的解集为$\left\{{m|-1<m<\frac{4}{3}}\right\}$.
点评 本题主要考查抽象函数的单调性证明和利用单调性定义解抽象不等式,利用定义法以及转化法是解决本题的关键.属于中档题.

练习册系列答案
相关题目
2.已知定义在R上的奇函数f(x)满足,当x≥0时,f(x)=2x+t(t为常数),则f(m)>0的一个充分不必要条件是( )
| A. | m<3 | B. | -2<m<2 | C. | m<2 | D. | m>2 |
9.随机变量ξ的分布列如下:
其中a,b,c成等差数列,若期望E(ξ)=$\frac{1}{3}$,则方差V(ξ)的值是$\frac{5}{9}$.
| ξ | -1 | 0 | 1 |
| P | a | b | c |
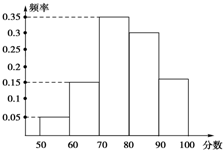 某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )
某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )