题目内容
四边形ABCD是正方形,A、B两点在抛物线y2=x上,C、D两点在直线y=x+4上.求正方形ABCD的面积.
思路解析:解方程组或设边长或由韦达定理求解. 解法一:设A(y12,y1),B(y22,y2),则 y2-y1=1 (y12-y22)2+(y1-y2)2=( 将①式代入②,得(y12-1+2y1-y12)2+(y1-1+y1)2= 化简,得4(2y1-1)2=(y1-y12-4)2. ∴4y1-2=y1-y12-4.∴y1=-2或y1=-1. ∴|AB|= 解法二:设A(y02,y0),ABCD边长为d,由于AC平行于y轴,且|AC|= 于是 (2)代入(1)中,得y02+3y0+2=0, ∴y0=-2或-1,∴|AB|= ∴S=|AB|2=50或18. 解法三:如下图所示,设ABCD的边长为d,则直线AB的方程为y=x+4- 由韦达定理,得y1+y2=1,y1y2=4- 又∵|AB|=d- ∴2[12-4(4- ∴正方形面积为18或50. 深化升华 从三个解法中可体会到,所设未知数不同.列方程的依据就不同,解答过程的繁简就不一样.应特别注意参数的设法,合理利用图形的特点以化简运算.![]() y2-y1=(y2+y1)(y2-y1),∴y2+y1=1.∴y2=1-y1. ①
y2-y1=(y2+y1)(y2-y1),∴y2+y1=1.∴y2=1-y1. ①![]() )2. ②
)2. ②![]() .
.![]() 或
或![]() ,∴S=|AB|2=50或18.
,∴S=|AB|2=50或18.![]() d,故C(y02,y0+
d,故C(y02,y0+![]() d),且B(y02+
d),且B(y02+![]() d,y0+
d,y0+![]() d).
d).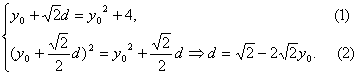
![]() 或
或![]() .
.![]() d.由
d.由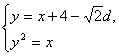 消去x,得y2-y+4-
消去x,得y2-y+4-![]() d=0.
d=0.
![]() d,
d,![]() ·
·![]() ,
,![]() d)]=d2.∴d2-8
d)]=d2.∴d2-8![]() d+30=0,解之,得d=3
d+30=0,解之,得d=3![]() 或d=5
或d=5![]() .
.

小学教学新思维检测卷快乐学习系列答案
新课标同步伴你学系列答案
8年沉淀1年突破单元同步夺冠卷系列答案

成龙计划高效课时学案系列答案
超能学典名牌中学期末突破一卷通系列答案
创佳绩课业巧点精练系列答案
单元期末满分大冲刺系列答案

全优课时作业系列答案
 中,E、F分别是
中,E、F分别是 、
、 的中点,G是正方形
的中点,G是正方形 的中心,画出空间四边形AEFG在该正方体的面上的正方向的平行投影的图形.
的中心,画出空间四边形AEFG在该正方体的面上的正方向的平行投影的图形.

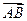 =4i-2j,
=4i-2j,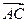 =7i+4j,
=7i+4j,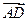 =3i+6j,求四边形ABCD的面积.
=3i+6j,求四边形ABCD的面积.